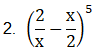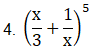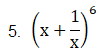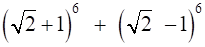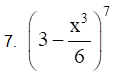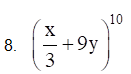Chapter 8 binomial theorem Questions and Answers: NCERT Solutions for Class 11th Maths

CBSE 10th Date sheet 2024      CBSE 12th Date Sheet 2024

Class 11 Maths Chapter 8: binomial theorem - Questions and Answers of NCERT Book Solutions

Exercise 8.1

---

Expand each of the expressions in Exercises 1 to 5.
1. (1 – 2x)5

Solution: From binomial theorem expansion we can write as (1 – 2x)5 = 5Co (1)5 – 5C1 (1)4 (2x) + 5C2 (1)3 (2x)2 – 5C3 (1)2 (2x)3 + 5C4 (1)1 (2x)4 – 5C5 (2x)5 = 1 – 5 (2x) + 10 (4x)2 – 10 (8x3) + 5 ( 16 x4) – (32 x5) = 1 – 10x + 40x2 – 80x3 + 80x4– 32x5

---

Solution: From binomial theorem, given equation can be expanded as

---

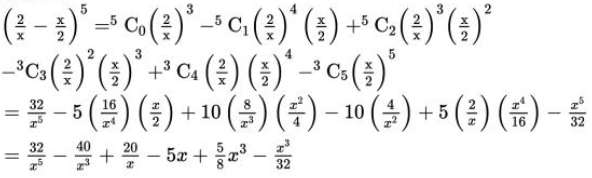
3. (2x – 3)6

Solution: From binomial theorem, given equation can be expanded as

---

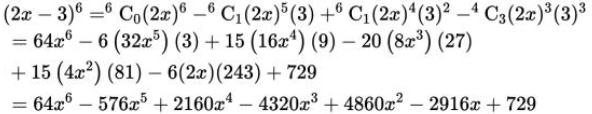
Solution: From binomial theorem, given equation can be expanded as

---

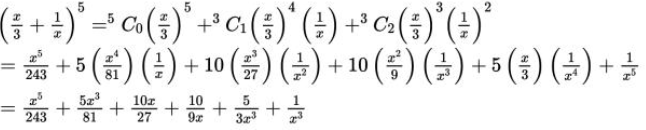
Solution: From binomial theorem, given equation can be expanded as

---

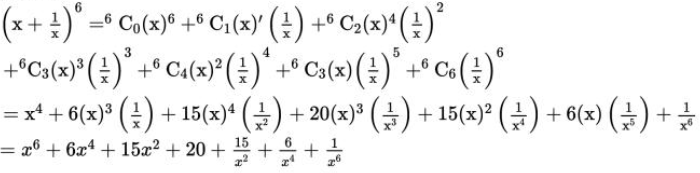
6. (96)3

Solution: Given (96)3 96 can be expressed as the sum or difference of two numbers and then binomial theorem can be applied. The given question can be written as 96 = 100 – 4 (96)3 = (100 – 4)3 = 3C0 (100)3 – 3C1 (100)2 (4) – 3C2 (100) (4)2– 3C3 (4)3 = (100)3 – 3 (100)2 (4) + 3 (100) (4)2 – (4)3 = 1000000 – 120000 + 4800 – 64 = 884736

---

7. (102)5

Solution: Given (102)5 102 can be expressed as the sum or difference of two numbers and then binomial theorem can be applied. The given question can be written as 102 = 100 + 2 (102)5 = (100 + 2)5 = 5C0 (100)5 + 5C1 (100)4 (2) + 5C2 (100)3 (2)2 + 5C3 (100)2 (2)3 + 5C4 (100) (2)4 + 5C5 (2)5 = (100)5 + 5 (100)4 (2) + 10 (100)3 (2)2 + 5 (100) (2)3 + 5 (100) (2)4 + (2)5 = 1000000000 + 1000000000 + 40000000 + 80000 + 8000 + 32 = 11040808032

---

8. (101)4

Solution: Given (101)4 101 can be expressed as the sum or difference of two numbers and then binomial theorem can be applied. The given question can be written as 101 = 100 + 1 (101)4 = (100 + 1)4 = 4C0 (100)4 + 4C1 (100)3 (1) + 4C2 (100)2 (1)2 + 4C3 (100) (1)3 + 4C4 (1)4 = (100)4 + 4 (100)3 + 6 (100)2 + 4 (100) + (1)4 = 100000000 + 4000000 + 60000 + 400 + 1 = 104060401

---

9. (99)5

Solution: Given (99)5 99 can be written as the sum or difference of two numbers then binomial theorem can be applied. The given question can be written as 99 = 100 -1 (99)5 = (100 – 1)5 = 5C0 (100)5 – 5C1 (100)4 (1) + 5C2 (100)3 (1)2 – 5C3 (100)2 (1)3 + 5C4 (100) (1)4 – 5C5 (1)5 = (100)5 – 5 (100)4 + 10 (100)3 – 10 (100)2 + 5 (100) – 1 = 1000000000 – 5000000000 + 10000000 – 100000 + 500 – 1 = 9509900499

---

10. Using Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.

Solution: By splitting the given 1.1 and then applying binomial theorem, the first few terms of (1.1)10000 can be obtained as (1.1)10000 = (1 + 0.1)10000 = (1 + 0.1)10000 C1 (1.1) + other positive terms = 1 + 10000 × 1.1 + other positive terms = 1 + 11000 + other positive terms > 1000 (1.1)10000 > 1000

---

11. Find (a + b)4 – (a – b)4. Hence, evaluate

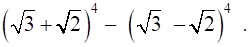
Solution: Using binomial theorem the expression (a + b)4 and (a – b)4, can be expanded (a + b)4 = 4C0 a4 + 4C1 a3 b + 4C2 a2 b2 + 4C3 a b3 + 4C4 b4 (a – b)4 = 4C0 a4 – 4C1 a3 b + 4C2 a2 b2 – 4C3 a b3 + 4C4 b4 Now (a + b)4 – (a – b)4 = 4C0 a4 + 4C1 a3 b + 4C2 a2 b2 + 4C3 a b3 + 4C4 b4 – [4C0 a4 – 4C1 a3 b + 4C2 a2 b2 – 4C3 a b3 + 4C4 b4] = 2 (4C1 a3 b + 4C3 a b3) = 2 (4a3 b + 4ab3) = 8ab (a2 + b2) Now by substituting a = √3 and b = √2 we get (√3 + √2)4 – (√3 – √2)4 = 8 (√3) (√2) {(√3)2 + (√2)2} = 8 (√6) (3 + 2) = 40 √6

---

12. Find (x + 1)6 + (x – 1)6. Hence or otherwise evaluate

Solution: Using binomial theorem the expressions, (x + 1)6 and (x – 1)6 can be expressed as (x + 1)6 = 6C0 x6 + 6C1 x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6 (x – 1)6 = 6C0 x6 – 6C1 x5 + 6C2 x4 – 6C3 x3 + 6C4 x2 – 6C5 x + 6C6 Now, (x + 1)6 – (x – 1)6 = 6C0 x6 + 6C1 x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6 – [6C0 x6 – 6C1 x5 + 6C2 x4 – 6C3 x3 + 6C4 x2 – 6C5 x + 6C6] = 2 [6C0 x6 + 6C2 x4 + 6C4 x2 + 6C6] = 2 [x6 + 15x4 + 15x2 + 1] Now by substituting x = √2 we get (√2 + 1)6 – (√2 – 1)6 = 2 [(√2)6 + 15(√2)4 + 15(√2)2 + 1] = 2 (8 + 15 × 4 + 15 × 2 + 1) = 2 (8 + 60 + 30 + 1) = 2 (99) = 198

---

13. Show that 9n+1 – 8n – 9 is divisible by 64, whenever n is a positive integer.

Solution: In order to show that 9n+1 – 8n – 9 is divisible by 64, it has to be show that 9n+1 – 8n – 9 = 64 k, where k is some natural number Using binomial theorem, (1 + a)m = mC0 + mC1 a + mC2 a2 + …. + m C m am For a = 8 and m = n + 1 we get (1 + 8)n+1 = n+1C0 + n+1C1 (8) + n+1C2 (8)2 + …. + n+1 C n+1 (8)n+1 9n+1 = 1 + (n + 1) 8 + 82 [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1] 9n+1 = 9 + 8n + 64 [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1] 9n+1 – 8n – 9 = 64 k Where k = [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1] is a natural number Thus, 9n+1 – 8n – 9 is divisible by 64, whenever n is positive integer. Hence the proof

---

14. Prove that

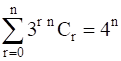
Solution:

---

Exercise 8.2

---

Find the coefficient of 1. x5 in (x + 3)8

Solution: The general term Tr+1 in the binomial expansion is given by Tr+1 = n C r an-r br Here x5 is the Tr+1 term so a= x, b = 3 and n =8 Tr+1 = 8Cr x8-r 3r…………… (i) For finding out x5 We have to equate x5= x8-r ⇒ r= 3 Putting value of r in (i) we get

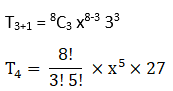
1512 x5 Hence the coefficient of x5= 151

---

2. a5b7 in (a – 2b)12 .

Solution: The general term Tr+1 in the binomial expansion is given by Tr+1 = n C r an-r br Here a = a, b = -2b & n =12 Substituting the values, we get Tr+1 = 12Cr a12-r (-2b)r………. (i) To find a5 We equate a12-r =a5 r = 7 Putting r = 7 in (i) T8 = 12C7 a5 (-2b)7

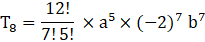
= -101376 a5 b7 Hence the coefficient of a5b7= -101376

---

3. (x2 – y)6

Solution: The general term Tr+1 in the binomial expansion is given by Tr+1 = n C r an-r br…….. (i) Here a = x2 , n = 6 and b = -y Putting values in (i) Tr+1 = 6Cr x 2(6-r) (-1)r yr

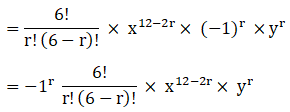
= -1r 6cr .x12 – 2r. yr

---

4. (x2 – y x)12, x ≠ 0.

Solution: The general term Tr+1 in the binomial expansion is given by Tr+1 = n C r an-r br Here n = 12, a= x2 and b = -y x Substituting the values we get Tn+1 =12Cr × x2(12-r) (-1)r yr xr

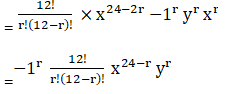
= -1r 12cr .x24 –2r. yr

---

5. Find the 4th term in the expansion of (x – 2y)12.

Solution: The general term Tr+1 in the binomial expansion is given by Tr+1 = n C r an-r br Here a= x, n =12, r= 3 and b = -2y By substituting the values we get T4 = 12C3 x9 (-2y)3

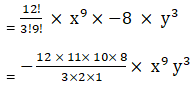
= -1760 x9 y3

---

6. Find the 13th term in the expansion of

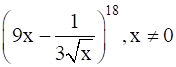
Solution:

---

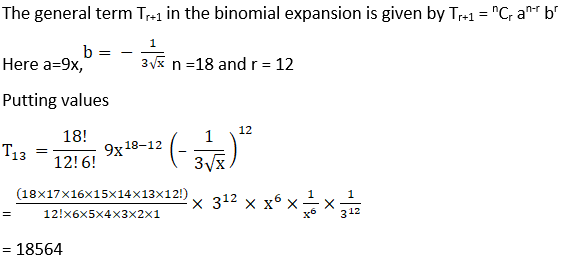
Solution:

---

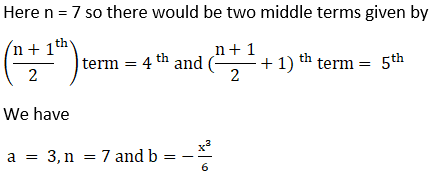
Solution:

---

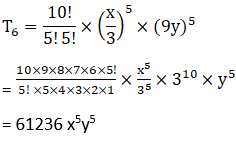
9. In the expansion of (1 + a)m+n, prove that coefficients of am and an are equal.

Solution: We know that the general term Tr+1 in the binomial expansion is given by Tr+1 = nCr an-r br Here n= m+n, a = 1 and b= a Substituting the values in the general form Tr+1 = m+n Cr 1m+n-r ar = m+n Cr ar…………. (i) Now we have that the general term for the expression is, Tr+1 = m+n Cr ar Now, For coefficient of am Tm+1 = m+n Cm am Hence, for coefficient of am, value of r = m So, the coefficient is m+n C m Similarly, Coefficient of an is m+n C n

---

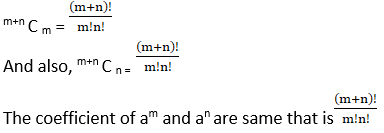
10. The coefficients of the (r – 1)th, rth and (r + 1)th terms in the expansion of (x + 1)n are in the ratio 1 : 3 : 5. Find n and r.

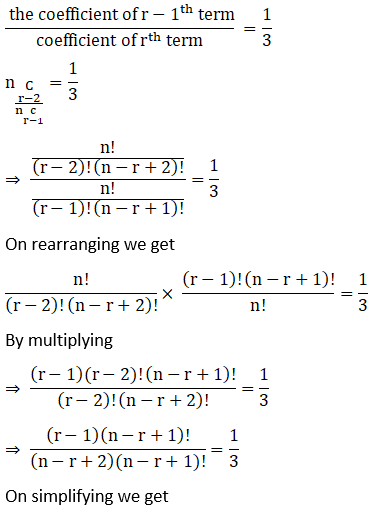
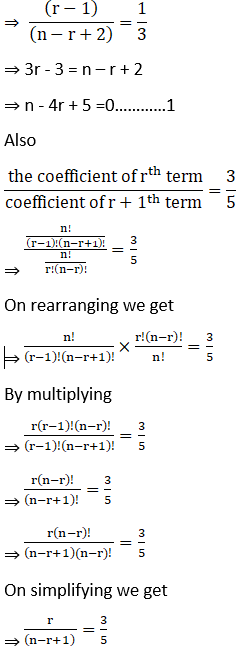
⇒ 5r = 3n – 3r + 3 ⇒ 8r – 3n – 3 =0………….2 We have 1 and 2 as n – 4r ± 5 =0…………1 8r – 3n – 3 =0…………….2 Multiplying equation 1 by number 2 2n -8r +10 =0……………….3 Adding equation 2 and 3 2n -8r +10 =0 -3n – 8r – 3 =0 ⇒ -n = -7 n =7 and r = 3

---

11. Prove that the coefficient of xn in the expansion of (1 + x)2n is twice the coefficient of xn in the expansion of (1 + x)2n – 1.

Solution: The general term Tr+1 in the binomial expansion is given by Tr+1 = nCr an-r br The general term for binomial (1+x)2n is Tr+1 = 2nCr xr …………………..1 To find the coefficient of xn r = n Tn+1 = 2nCn xn The coefficient of xn = 2nCn The general term for binomial (1+x)2n-1 is Tr+1 = 2n-1Cr xr To find the coefficient of xn Putting n = r Tr+1 = 2n-1Cr xn The coefficient of xn = 2n-1Cn We have to prove Coefficient of xn in (1+x)2n = 2 coefficient of xn in (1+x)2n-1 Consider LHS = 2nCn

---

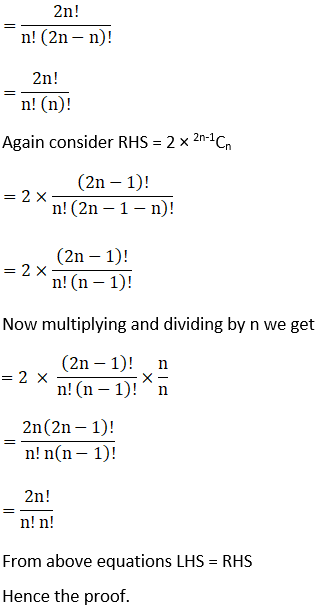
12. Find a positive value of m for which the coefficient of x2 in the expansion (1 + x)m is 6.

Solution: The general term Tr+1 in the binomial expansion is given by Tr+1 = nCr an-r br Here a = 1, b = x and n = m Putting the value Tr+1 = m Cr 1m-r xr = m Cr xr We need coefficient of x2 ∴ putting r = 2 T2+1 = mC2 x2 The coefficient of x2 = mC2 Given that coefficient of x2 = mC2 = 6

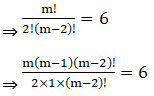
⇒ m (m – 1) = 12 ⇒ m2– m – 12 =0 ⇒ m2– 4m + 3m – 12 =0 ⇒ m (m – 4) + 3 (m – 4) = 0 ⇒ (m+3) (m – 4) = 0 ⇒ m = – 3, 4 We need positive value of m so m = 4

---

Last Updated on: Mar 07, 2024