Chapter 5 Laws of Motion Questions and Answers: NCERT Solutions for Class 11th Physics (Partnership Physics )
Class 11 Physics (Partnership Physics ) Chapter 5: Laws of Motion - Questions and Answers of NCERT Book Solutions.
1. Give the magnitude and direction of the net force acting on a.drop of rain falling down with a constant speed,
Ans: The net force is zero.
As the speed of the rain drop falling down is constant, its acceleration is zero.
Therefore, from Newton’s second law of motion, the net force acting on the rain drop is zero.
a cork of mass 10g10g floating on water,
Ans: The net force is zero.
It is known that the weight of a cork floating on water acts downward.
The weight of the cork is balanced by buoyant force exerted by the water in the upward direction.
Therefore, no net force acts on the floating cork.
a kite skilfully held stationary in the sky,
Ans: The net force is zero.
The kite is stationary in the sky indicates that it is not moving.
Therefore, from Newton’s first law of motion, the net force acting on the kite is zero.
a car moving with a constant velocity of 30km/h30km/h on a rough road,
Ans: The net force is zero.
As the car is moving with constant velocity, its acceleration is zero.
Therefore, from Newton’s second law of motion, net force acting on the car is equal to zero.
a high-speed electron in space far from all material objects, and free of electric and magnetic fields.
Ans: The net force is zero.
As the high speed electron is free from the influence of all the fields, no net force acts on the electron.
2. A pebble of mass 0.05kg 0.05kg is thrown vertically upwards. Ignore air resistance and give the direction and magnitude of the net force on the pebble,
during its upward motion,
Ans: It is known that,
Acceleration due to gravity always acts downward irrespective of the direction of motion of an object. The only force that acts on the pebble thrown vertically upward during its upward motion is the gravitational force.
From Newton’s second law of motion: F=m×aF=m×a
Where,
FF is the net force
mm is the mass of the pebble, m=0.05kgm=0.05kg
a is the acceleration due to gravity, a=g=10m/s−2a=g=10m/s−2
⇒F=0.05×10=0.5N⇒F=0.05×10=0.5N
Therefore, the net force on the pebble is 0.5N0.5N and this force acts in the downward direction.
during its downward motion,
Ans: The only force that acts on the pebble during its downward motion is the gravitational force.
Therefore, the net force on the pebble in its downward direction is same as in upward direction i.e., 0.5N0.5N and this force
acts in the downward direction.
at the highest point where it is momentarily at rest. Do your answers change if the pebble was thrown at an angle of 45∘45∘ with the horizontal direction?
Ans: When the pebble is thrown at an angle of 45∘45∘with the horizontal, it will have both the horizontal and vertical components of velocity.
At the highest point, only the vertical component of velocity becomes zero. However, the pebble will have the horizontal component of velocity throughout its motion. This component of velocity produces no effect on the net force acting on the pebble.
Therefore, the net force on the pebble is 0.5N0.5N.
3. Neglect air resistance throughout and give the magnitude and direction of the net force acting on a stone of mass 0.1kg0.1kg ,
a.just after it is dropped from the window of a stationary train,
Ans: It is given that,
Mass of the stone, m=0.1kg
m=0.1kg
Acceleration of the stone, a=g=10m/s2
a=g=10m/s2
From Newton’s second law of motion,
The net force acting on the stone is F=ma=mgF=ma=mg
⇒F=0.1×10=1N⇒F=0.1×10=1N
It is known that acceleration due to gravity always acts in the downward direction.
Therefore, the magnitude of force is 1N1N and its direction is vertically downward.
just after it is dropped from the window of a train running at a constant velocity of 36km/h36km/h,
Ans: It is given that,
The train is moving with a constant velocity.
Therefore, its acceleration is zero in the direction of its motion, i.e. in the horizontal direction.
Thus, no force is acting on the stone in the horizontal direction.
The net force acting on the stone is because of acceleration due to gravity and it always acts vertically downward.
Therefore, the magnitude of force is 1N1N and its direction is vertically downward.
just after it is dropped from the window of a train accelerating with 1ms−21ms−2
Ans: It is given that,
The train is accelerating at the rate of 1ms−21ms−2.
Therefore, the net force acting on the stone is F′=ma=0.1×1=1NF′=ma=0.1×1=1N
This force is acting in the horizontal direction. Now, when the stone is dropped, the horizontal force stops acting on the stone. This is because of the fact that the force acting on a body at an instant depends on the situation at that instant and not on earlier situations.
Therefore, the net force acting on the stone is given only by acceleration due to gravity i.e., F=mg=1NF=mg=1N.
Therefore, the magnitude of force is 1N1N and its direction is vertically downward.
lying on the floor of a train which is accelerating with 1ms−21ms−2, the stone being at rest relative to the train.
Ans: It is known that,
The weight of the stone is balanced by the normal reaction of the floor. The only acceleration is provided by the horizontal motion of the train.
Acceleration of the train, a=1ms−2a=1ms−2
The net force acting on the stone will be in the direction of motion of the train.
Magnitude: F=ma=0.1×1=0.1NF=ma=0.1×1=0.1N
Therefore, the magnitude of force is 0.1N0.1N and its direction is in the direction of motion of the train.
4. One end of a string of length ll is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed vv the net force on the particle (directed towards the centre) is:
i. TT,
ii. T−mv2lT−mv2l ,
iii. T+mv2lT+mv2l,
iv. 00
TT is the tension in the string. (Choose the correct alternative).
Ans: (i) TT
The centripetal force of a particle connected to a string revolving in a circular path around a centre is provided by the tension produced in the string.
Therefore, the net force on the particle is the tension TT , i.e.,
F=T=mv2lF=T=mv2l
Where FF is the net force acting on the particle.
5. A constant retarding force of 50N50N is applied to a body of mass 20kg20kg moving initially with a speed of 15ms−115ms−1 . How long does the body take to stop?
Ans: It is given that,
Retarding force, F=50N
F=50N
Mass of the body, m=20kgm=20kg
Initial velocity of the body, u=15m/s
u=15m/s
Final velocity of the body, v=0v=0
From Newton’s second law of motion,
The acceleration (a)(a) produced in the body: F=maF=ma ,
⇒−50=20×a⇒−50=20×a
⇒a=−5020=−2.5ms−2⇒a=−5020=−2.5ms−2
From the first equation of motion,
The time (t)(t) taken by the body to come to rest: v=u+atv=u+at
⇒0=15+(−2.5)t⇒0=15+(−2.5)t
⇒t=−15−2.5=6s⇒t=−15−2.5=6s
Therefore, the time taken by the body to stop is 6s6s.
6. A constant force is acting on a body of mass 3.0kg3.0kg changes its speed from 2.0ms−12.0ms−1 to 3.0ms−13.0ms−1 in 25s25s . The direction of the motion of the body remains unchanged. What is the magnitude and direction of the force?
Ans: It is given that,
Mass of the body, m=3kgm=3kg
Initial speed of the body, u=2m/s
u=2m/s
Final speed of the body, v=3.5m/s
v=3.5m/s
Time, t=25st=25s
From the first equation of motion,
The acceleration (a)(a) produced in the body: v=u+atv=u+at
⇒a=v−ut⇒a=v−ut
⇒a=3.5−225=1.525=0.6ms−2⇒a=3.5−225=1.525=0.6ms−2
From Newton’s second law of motion,
Force, F=maF=ma
⇒F=3×0.06=0.18N
⇒F=3×0.06=0.18N
As the application of force does not change the direction of the body, the net force acting on the body is in the direction of its motion.
Therefore, the magnitude of force is 0.18N0.18N and direction is along the direction of motion.
In ΔOPSΔOPS,
7. A body of mass 5kg5kg is acted upon by two perpendicular forces 8N8N and 6N6N. Give the magnitude and direction of the acceleration of the body.
Ans: It is given that,
Mass of the body, m=5kgm=5kg
Representation of given data:
 Law of Vectors
Law of Vectors
Resultant of two forces 8N8N and 6N6N, R=(8)2+(−6)2−−−−−−−−−−√R=(8)2+(−6)2
⇒R=64+36−−−−−−√⇒R=64+36
⇒R=10N⇒R=10N
Angle made by RR with the force of 8N8N
θ=tan−1(−68)=−36.87∘θ=tan−1(−68)=−36.87∘
The negative sign indicates that θθ is in the clockwise direction with respect to the force of magnitude 8N8N.
From Newton’s second law of motion,
The acceleration (a)(a) produced in the body: F=maF=ma
a=Fm=105=2ms−2a=Fm=105=2ms−2
Therefore, the magnitude of acceleration is 2ms−22ms−2 and direction is 37∘37∘ with a force of 8N8N.
8. The driver of a three-wheeler moving with a speed of 36km/h36km/h sees a child standing in the middle of the road and brings his vehicle to rest in 4.0s4.0s just in time to save the child. What is the average retarding force on the vehicle? The mass of the three-wheeler is 400kg400kg and the mass of the driver is 65kg65kg.
Ans: It is given that,
Initial speed of the three-wheeler, u=36 km/h
u=36 km/h
Final speed of the three-wheeler, v=0m/s
v=0m/s
Time, t=4st=4s
Mass of the three-wheeler, m=400kgm=400kg
Mass of the driver, m′=65kgm′=65kg
Total mass of the system, M=400+65=465kg
M=400+65=465kg
From the first law of motion,
The acceleration (a)(a) of the three-wheeler can be calculated from: v=u+atv=u+at
⇒a=v−ut=0−104⇒a=v−ut=0−104
⇒a=−2.5m/s2⇒a=−2.5m/s2
The negative sign indicates that the velocity of the three-wheeler is decreasing with time.
From Newton’s second law of motion,
The net force acting on the three-wheeler can be calculated as: F=maF=ma
⇒F=465×(−2.5)⇒F=465×(−2.5)
⇒F=−1162.5N⇒F=−1162.5N
The negative sign indicates that the force is acting against the direction of motion of the three-wheeler.
Therefore, the average retarding force on the vehicle is −1162.5N−1162.5N.
9. A rocket with a lift-off mass 20,000kg20,000kg is blasted upwards with an initial acceleration of 5.0ms−25.0ms−2. Calculate the initial thrust (force) of the blast.
Ans: It is known that,
Mass of the rocket, m=20,000kgm=20,000kg
Initial acceleration, a=5ms−2a=5ms−2
Acceleration due to gravity, g=10ms−2g=10ms−2
By using Newton’s second law of motion,
The net force (thrust) acting on the rocket can be written as:
F−mg=maF−mg=ma
⇒F=m(g+a)⇒F=m(g+a)
⇒F=20000(10+5)=20000×15⇒F=20000(10+5)=20000×15
⇒F=3×105N⇒F=3×105N
Therefore, the initial thrust(force) of the blast is 3×105N3×105N.
10. A body of mass 0.40kg 0.40kg moving initially with a constant speed of 10ms−110ms−1 subject to a constant force of 8.0N8.0N directed towards the south for 30s30s. Take the instant the force is applied to be t=0t=0 , the position of the body at that time to be predict its position at t=−5 s, 25 s, 100 s t=−5 s, 25 s, 100 s
Ans: It is given that,
Mass of the body, m=0.40kgm=0.40kg
Initial speed of the body, u=10m/s
u=10m/s
due north
Force acting on the body, F=−8.0NF=−8.0N
Acceleration produced in the body, a=Fma=Fm
At t=0t=0
⇒a=−80.4=−20ms−2⇒a=−80.4=−20ms−2
At t=−5st=−5s
Acceleration, a′=0a′=0 and u=10m/su=10m/s
s=ut+12a′t2s=ut+12a′t2
⇒s=10×(−5)=−50m⇒s=10×(−5)=−50m
At t=25st=25s
Acceleration, a=−20ms−2a=−20ms−2 and u=10m/su=10m/s
s′=ut′+12a(t′)2s′=ut′+12a(t′)2
⇒s′=10×(25)+12×(−20)(25)2⇒s′=10×(25)+12×(−20)(25)2
⇒s′=250+(−6250)⇒s′=250+(−6250)
⇒s′=−6000m⇒s′=−6000m
At t=100st=100s
For 0≤t≤30s0≤t≤30s, a=−20ms−2a=−20ms−2 and u=10m/su=10m/s
s1=ut+12at2s1=ut+12at2
⇒s1=10×30+12×(−20)×(30)2⇒s1=10×30+12×(−20)×(30)2
⇒s1=300−9000⇒s1=300−9000
⇒s1=8700m⇒s1=8700m
For 30s≤t≤100s30s≤t≤100s
First equation of motion: v=u+atv=u+at
⇒v=10+(−20)×30⇒v=10+(−20)×30
⇒v=−590ms−1⇒v=−590ms−1
Velocity of body after 30s=−590m/s30s=−590m/s
For motion between 30s30s to 100s100s i.e., in 70s70s
s2=vt+12a′t2s2=vt+12a′t2
s2=−590×70=−41300ms2=−590×70=−41300m
Total distance, s′′=s1+s2s″=s1+s2
⇒s′′=−8700+(−41300)=−50000m⇒s″=−8700+(−41300)=−50000m
Therefore, the position of the body at t=−5st=−5s is −50m−50m at t=25st=25s is −6000m−6000m and at t=100st=100s is−50,000m−50,000m.
11. A truck starts from rest and accelerates uniformly at 2.0ms−22.0ms−2. At t=10st=10s, a stone is dropped by a person standing on the top of the truck (6m6m high from the ground). Neglect air resistance. What are the
velocity, and
Ans: It is given that,
Initial velocity of the truck, u=0u=0 (Initially at rest)
Acceleration, a=2ms−2a=2ms−2
Time, t=10st=10s
From first equation of motion: v=u+atv=u+at
⇒v=0+2×10=20m/s⇒v=0+2×10=20m/s
Therefore, the final velocity of the truck and the stone is20m/s20m/s.
At t=11st=11s:
The horizontal component (vx)(vx) of velocity, in the absence of air resistance, remains unchanged, i.e. vx=20m/s
vx=20m/s
.
The vertical component of velocity (vy)(vy) of the stone is given by the first equation of motion as:
vy=u+ayδtvy=u+ayδt
Where,
δt=11−10=1sδt=11−10=1s
a=g=10m/s2a=g=10m/s2
⇒vy=0+10×1=10m/s2⇒vy=0+10×1=10m/s2
The resultant velocity (v)(v) of the stone is:
Two Velocities of Different Magnitude
⇒v=v2x+v2y−−−−−−√⇒v=vx2+vy2
⇒v=202+102−−−−−−−−√=400+100−−−−−−−−√⇒v=202+102=400+100
⇒v=500−−−√=22.36m/s⇒v=500=22.36m/s
Consider θθ as the angle made by the resultant velocity with the horizontal component of velocity, vxvx.
⇒tanθ=(vyvx)⇒tanθ=(vyvx)
⇒θ=tan−1(vyvx)⇒θ=tan−1(vyvx)
⇒θ=tan−1(1020)⇒θ=tan−1(1020)
⇒θ=tan−1(0.5)⇒θ=tan−1(0.5)
⇒θ=26.57∘⇒θ=26.57∘
Therefore, the magnitude of resultant velocity is 22.36m/s22.36m/s making an angle of 26.57∘26.57∘ with the horizontal component of velocity.
acceleration of the stone at t=11st=11s?
Ans: When the stone is dropped from the truck, the horizontal force acting on it becomes zero. However, the stone continues to move under the influence of gravity.
Therefore, the acceleration of the stone is 10ms−210ms−2 and it acts vertically downward.
12. A bob of mass 0.1kg 0.1kg hung from the ceiling of a room by a string 2m2m long is set into oscillation. The speed of the bob at its mean position is 1ms−21ms−2. What is the trajectory of the bob if the string is cut when the bob is
at one of its extreme positions,
Ans: If the string is cut when the bob is at one of its extremes then the bob will fall vertically on the ground.
Therefore, at the extreme position, the velocity of the bob becomes zero.
at its mean position.
Ans: If the string is cut when the bob is at its mean position then the bob will trace a projectile path having the horizontal components of velocity only.
The direction of this velocity is tangential to the arc formed by the oscillating bob. At the mean position, the velocity of the bob is 1m/s1m/s.
Therefore, it will follow a parabolic path.
13. What would be the readings on the scale of a man of mass 70kg 70kg stands on a weighing scale in a lift which is moving
upwards with a uniform speed of 10ms−110ms−1,
Ans: It is given that,
Mass of the man, m=70kgm=70kg
Acceleration, a=0a=0(uniform speed)
From Newton’s second law: R−mg=maR−mg=ma
Where,
mama is the net force acting on the man.
⇒R−70×10=0⇒R−70×10=0
⇒R=700N⇒R=700N
Reading on the weighing scale=700g=70010=70kg=700g=70010=70kg
Therefore, the mass of the man, m=70kgm=70kg
downwards with a uniform acceleration of 5ms−25ms−2,
Ans: Acceleration,a=5m/s2a=5m/s2 downward
From Newton’s second law: R=m(g−a)R=m(g−a)
⇒R=70(10−5)=70×5⇒R=70(10−5)=70×5
⇒R=350N⇒R=350N
Reading on the weighing scale=350g=35010=35kg=350g=35010=35kg
Therefore, the mass of the man, m=35kgm=35kg
upwards with a uniform acceleration of 5ms−25ms−2.
Ans: Acceleration,a=5m/s2a=5m/s2 upward
From Newton’s second law: R=m(g+a)R=m(g+a)
⇒R=70(10+5)=70×15⇒R=70(10+5)=70×15
⇒R=1050N⇒R=1050N
Reading on the weighing scale=1050g=105010=105kg=1050g=105010=105kg
Therefore, the mass of the man, m=105kgm=105kg
What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?
Ans: When the lift moves freely under gravity,
Acceleration, a=g=10ms−2a=g=10ms−2
From Newton’s second law: R=m(g−a)R=m(g−a)
⇒R=70(10−10)=0⇒R=70(10−10)=0
Reading on the weighing scale=0g=010=0kg=0g=010=0kg
Therefore, the man will be in a state of weightlessness.
14. Figure shows the position-time graph of a particle of mass 4kg4kg . Consider one-dimensional motion only and find the
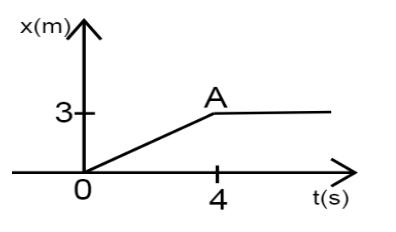
force on the particle for t<0,t>4st<0,t>4s,0
Ans: For t<0t<0 :
From the given graph, it is observed that the position of the particle is coincident with the time axis. It indicates that the displacement of the particle in this time interval is zero.
Therefore, the force acting on the particle is zero.
For t>4st>4s :
From the given graph, it is observed that the position of the particle is parallel to the time axis. It indicates that the particle is at rest at a distance of 3m3m from the origin.
Therefore, no force acts on the particle.
For 0
From the given position-time graph, it is observed that it has a constant slope. Thus, the acceleration produced in the particle is zero.
Therefore, the force acting on the particle is zero.
impulse at t=0t=0 and t=4st=4s ?
Ans: At t=0t=0:
Impulse=Change in momentum=mv−mu
Impulse=Change in momentum=mv−mu
Mass of the particle, m=4kgm=4kg
Initial velocity of the particle, u=0u=0
Final velocity of the particle, v=34m/sv=34m/s
Impulse =4(34−0)=3kgms−1=4(34−0)=3kgms−1
At t=4st=4s:
Initial velocity of the particle, u=34m/su=34m/s
Final velocity of the particle, v=0v=0
Impulse=4(0−34)=−3kgms−1
=4(0−34)=−3kgms−1
Therefore, the impulse at t=0t=0 is 3kgms−13kgms−1 and at t=4st=4sis −3kgms−1−3kgms−1.
From the given graph, it is observed that the position of the particle is coincident with the time axis. It indicates that the displacement of the particle in this time interval is zero.
Therefore, the force acting on the particle is zero.
For t>4st>4s :
From the given graph, it is observed that the position of the particle is parallel to the time axis. It indicates that the particle is at rest at a distance of 3m3m from the origin.
Therefore, no force acts on the particle.
For 0
Therefore, the force acting on the particle is zero.
impulse at t=0t=0 and t=4st=4s ?
Ans: At t=0t=0:
Impulse=Change in momentum=mv−mu
Impulse=Change in momentum=mv−mu
Mass of the particle, m=4kgm=4kg
Initial velocity of the particle, u=0u=0
Final velocity of the particle, v=34m/sv=34m/s
Impulse =4(34−0)=3kgms−1=4(34−0)=3kgms−1
At t=4st=4s:
Initial velocity of the particle, u=34m/su=34m/s
Final velocity of the particle, v=0v=0
Impulse=4(0−34)=−3kgms−1
=4(0−34)=−3kgms−1
Therefore, the impulse at t=0t=0 is 3kgms−13kgms−1 and at t=4st=4sis −3kgms−1−3kgms−1.
15. Two bodies of masses 10kg10kg and 20kg20kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. What is the tension in the string if a horizontal force F=600NF=600N is applied along the direction of string to a) A, b) B along the direction of the string. What is the tension in the string in each case?
A,
Ans: It is given that,
Horizontal force, F=600NF=600N
Mass of body A, m1=10kgm1=10kg
Mass of body B, m2=20kgm2=20kg
Total mass of the system, m=m1+m2=30kgm=m1+m2=30kg
From Newton’s second law of motion,
The acceleration (a)(a) produced in the system is: F=maF=ma
⇒a=Fm=60030=20ms−2⇒a=Fm=60030=20ms−2
When force FF is applied on body A:
16. Two masses 8kg8kg and 12kg12kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley. Find the acceleration of the masses, and the tension in the string when the masses are released.
Answer. Smaller mass, m1=8kgm1=8kg
Larger mass, m2=12kgm2=12kg
Tension in the string =T=T
Mass m2
m2
, owing to its weight, moves downward with acceleration aa, and mass moves m1m1upward.
Applying Newton’s second law of motion to the system of each mass:
For mass m1m1:
The equation of motion can be written as: T−m1g=ma
T−m1g=ma
.......(1)(1)
For mass m2m2:
The equation of motion can be written as: m2g−T=m2a
m2g−T=m2a
........(2)(2)
Adding equations (1)(1) and (2)(2), we get:
(m2−m1)g=(m1+m2)a(m2−m1)g=(m1+m2)a
⇒a=(m2−m1m2+m1)g⇒a=(m2−m1m2+m1)g ........(3)(3)
⇒a=(12−812+8)×10=420×10⇒a=(12−812+8)×10=420×10
⇒a=2ms−2⇒a=2ms−2
Thus, the acceleration of the masses is 2ms−22ms−2 . Substituting the value of aa in equation (2)(2):
⇒m2g−T=m2(m2−m1m2+m1)g
⇒m2g−T=m2(m2−m1m2+m1)g
⇒T=(m2−m22−m1m2m2+m1)g
⇒T=(m2−m22−m1m2m2+m1)g
⇒T=(2m1m2m1+m2)g
⇒T=(2m1m2m1+m2)g
⇒T=(2×12×812+8)×10
⇒T=(2×12×812+8)×10
⇒T=96N
⇒T=96N
Thus, the tension in the string is 96N96N.
17. A nucleus is at rest in the laboratory frame of reference. Show that if it disintegrates into two smaller nuclei the products must move in opposite directions.
Ans: Consider mm, m1m1 and m2m2 as the respective masses of the parent nucleus and the two daughter nuclei. The parent nucleus is at rest.
Initial momentum of the system (parent nucleus) =0=0
Let v1v1 and v2v2 be the respective velocities of the daughter nuclei having masses m1m1 and m2m2.
Total linear momentum of the system after disintegration=m1v1+m2v2=m1v1+m2v2
From the law of conservation of momentum:
18. Two billiard balls each of mass 0.05kg0.05kg moving in opposite directions with speed 6ms−16ms−1 collide and rebound with the same speed. What is the impulse imparted to each ball due to the other?
Ans: It is given that,
Mass of each ball=0.05kg=0.05kg
Initial velocity of each ball=6m/s=6m/s
Magnitude of the initial momentum of each ball, pi=0.3kgms−1pi=0.3kgms−1
After collision, the balls change their directions of motion without changing the
magnitudes of their velocity.
Final momentum of each ball, pf=−0.3kgms−1pf=−0.3kgms−1
Impulse imparted to each ball== Change in the momentum of the system
⇒Impulse=pf−pi⇒Impulse=pf−pi
⇒Impulse=−0.3−0.3=−0.6kgms−1⇒Impulse=−0.3−0.3=−0.6kgms−1
The negative sign indicates that the impulses imparted to the balls are opposite in direction.
19. A shell of mass 0.020kg 0.020kg is fired by a gun of mass 100kg 100kg . If the muzzle speed of the shell is 80ms−180ms−1 what is the recoil speed of the gun?
Ans: It is given that,
Mass of the gun, M=100kgM=100kg
Mass of the shell, m=0.020kgm=0.020kg
Muzzle speed of the shell, v=80m/sv=80m/s
Recoil speed of the gun =V=V.
Both the gun and the shell are at rest initially.
Initial momentum of the system=0=0
Final momentum of the system=mv−MV=mv−MV
Here, the negative sign appears because the directions of the shell and the gun are opposite to each other.
From the law of conservation of momentum:
Final momentum=Initial momentum
Final momentum=Initial momentum
mv−MV=0mv−MV=0
⇒V=mvM⇒V=mvM
⇒V=0.020×80100×1000=0.016m/s⇒V=0.020×80100×1000=0.016m/s
Therefore, the recoil speed of the gun is 0.016m/s0.016m/s.
20. A batsman deflects a ball by an angle of 45∘45∘ without changing its initial speed which is equal to 54km/h54km/h . What is the impulse imparted to the ball? (Mass of the ball is 0.15kg0.15kg)
Ans: The given situation can be represented as:
Deflection of a Ball Hit by a Batsman
Where,
AO=AO= Incident path of the ball
OB=OB= Path followed by the ball after a deflection
∠AOB=∠AOB= Angle between the incident and deflected paths of the ball=45∘=45∘
∠AOB=∠BOP=22.5∘=θ∠AOB=∠BOP=22.5∘=θ
Initial and final velocities of the ball=v=v
The horizontal component of the initial velocity=vcosθ=vcosθ along RORO
Vertical component of the initial velocity=vsinθ=vsinθ along POPO
The horizontal component of the final velocity=vcosθ=vcosθ along OSOS
The vertical component of the final velocity =vsinθ=vsinθ along OPOP
The horizontal components of velocities suffer no change. The vertical components of velocities are in opposite directions.
It is known that Impulse imparted to the ball== Change in the linear momentum of the ball.
Impulse=mvcosθ−(−mvcosθ)=2mvcosθImpulse=mvcosθ−(−mvcosθ)=2mvcosθ
It is given that,
Mass of the ball, m=0.15kgm=0.15kg
Velocity of the ball, v=54km/h=54×518=15m/sv=54km/h=54×518=15m/s
Impulse=2×0.15×15cos22.5∘=4.16kgms−1=2×0.15×15cos22.5∘=4.16kgms−1
Therefore, impulse imparted to the ball is 4.16kgms−14.16kgms−1 .
21. A stone of mass 0.25kg0.25kg tied to the end of a string is whirled round in a circle of radius 1.5m1.5m with a speed of 40rev./min40rev./min in a horizontal plane. What is the tension in the string? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200N200N?
Ans: It is given that,
Mass of the stone, m=0.25kgm=0.25kg
Radius of the circle, r=1.5mr=1.5m
Number of revolution per second, n=4060=23rpsn=4060=23rps
Angular velocity, ω=vr=2πnω=vr=2πn ........(1)(1)
\
The centripetal force for the stone is provided by the tension TT , in the string, i.e., T=FCentripetalT=FCentripetal
⇒mv2r=mrω2=mr(2πn)2⇒mv2r=mrω2=mr(2πn)2
⇒FCentripetal=0.25×1.5×(2×3.14×23)2⇒FCentripetal=0.25×1.5×(2×3.14×23)2
⇒FCentripetal=6.57N⇒FCentripetal=6.57N
Maximum tension in the string, Tmax=200NTmax=200N
Tmax=mv2maxrTmax=mvmax2r
⇒vmax=Tmax×rm−−−−−√⇒vmax=Tmax×rm
⇒vmax=200×1.50.25−−−−−−√⇒vmax=200×1.50.25
⇒vmax=1200−−−−√=34.64m/s
⇒vmax=1200=34.64m/s
Thus, the maximum speed of the stone is 34.64m/s
34.64m/s
.
22. If, in Exercise 21, the speed of the stone is increased beyond the maximum permissible value, and the string breaks suddenly, which of the following correctly describes the trajectory of the stone after the string breaks:
(i)the stone moves radially out wards,
(ii)the stone flies off tangentially from the instant the string breaks,
(III)the stone flies off at an angle with the tangent whose magnitude depends on the speed of the particle?
Ans: (ii)(ii)
From the first law of motion, the direction of velocity vector is tangential to the path of the stone at that instant. So, if the string breaks, the stone will move in the direction of the velocity at that instant.
Therefore, the stone will fly off tangentially from the instant the string breaks.
23. Explain why
a horse cannot pull a cart and run in empty space,
Ans: In order to pull a cart, a horse pushes the ground backward with some force. The ground in turn exerts an equal and opposite reaction force upon the feet of the horse.
This reaction force causes the horse to move forward. An empty space is devoid of any such reaction force.
Hence, a horse cannot pull a cart and run in empty space.
b.passengers are thrown forward from their seats when a speeding bus stops suddenly,
Ans: If a speeding bus stops suddenly, the lower portion of a passenger’s body, which is in contact with the seat, suddenly comes to rest. However, the upper portion tends to remain in motion (as per the first law of motion).
So, the passenger’s upper body is thrown forward in the direction in which the bus was moving.
c. it is easier to pull a lawn mower than to push it,
Ans: While pulling a lawn mower, a force at an angle θθ is applied on it, as shown in the following figure:
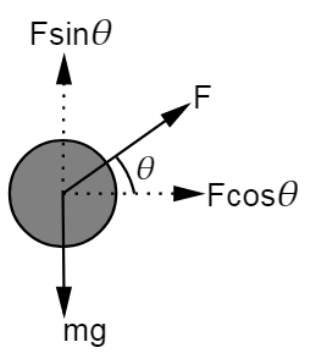
The vertical component of this applied force acts upward. This reduces the effective weight of the mower.
While pushing a lawn mower, a force at an angle θθ is applied on it, as shown in the following figure:
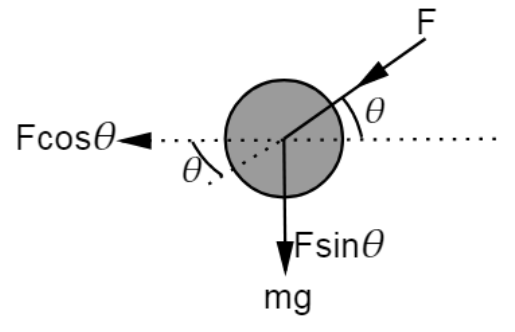
In this case, the vertical component of the applied force acts in the direction of the weight of the mower. This increases the effective weight of the mower.
As the effective weight of the lawn mower is lesser in the first case, pulling the lawn mower is easier than pushing it.
From Newton’s second law of motion: F=ma=mΔvΔtF=ma=mΔvΔt ........(1)(1)
Where,
F=F= Stopping force experienced by the cricketer as he catches the ball
m=m= Mass of the ball
t=t= Time of impact of the ball with the hand
From equation (1)(1)it can be observed that the impact force is inversely proportional to the impact time, i.e., F<1ΔtF<1Δt ........(2)(2)
Equation (2)(2) shows that the force experienced by the cricketer decreases if the time of impact increases and vice versa.
Therefore, it is easier to pull a lawn mower than to push it.
d. a cricketer moves his hands backwards while holding a catch.
Ans: While taking a catch, a cricketer moves his hand backward so as to increase the time of impact ΔtΔt. This in turn results in the decrease in the stopping force, thereby preventing the hands of the cricketer from getting hurt.
Therefore, a cricketer moves his hands backwards while holding a catch.
24. Figure shows the position-time graph of a body of mass 0.04kg0.04kg . Suggest a suitable physical context for this motion. What is the time between two consecutive impulses received by the body? What is the magnitude of each impulse?
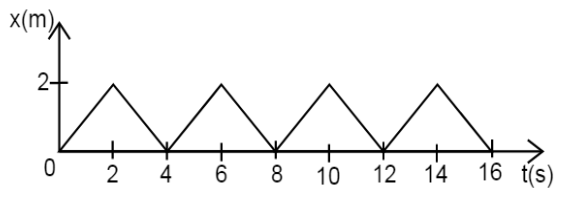
Ans: In the given case, a ball is rebounding between two walls located between at x=0x=0 and x=2cmx=2cm ; after every 2s2s, the ball receives an impulse of magnitude 0.08×10−2kgms−10.08×10−2kgms−1 from the walls.
The given graph shows that a body changes its direction of motion after every 2s2s.
This situation can be visualized as a ball rebounding to and fro between two stationary walls situated between positions x=0x=0 and x=2cmx=2cm.
As the slope of the x-t graph reverses after every 2s2s , the ball collides with a wall after every 2s2s. Therefore, ball receives an impulse after every 2s2s.
Mass of the ball, m=0.04kgm=0.04kg
The slope of the graph gives the velocity of the ball.
From the graph, initial velocity is u=(2−0)×10−2(2−0)=10−2m/su=(2−0)×10−2(2−0)=10−2m/s
Velocity of the ball before collision, u=10−2m/su=10−2m/s
Velocity of the ball after collision, v=−10−2m/sv=−10−2m/s,
(The negative sign arises as the ball reverses its direction of motion.)
Magnitude of impulse = Change in momentum
⇒|mv−mu|=∣∣0.04(−10−2−10−2)∣∣⇒|mv−mu|=|0.04(−10−2−10−2)|
⇒0.08×10−2kgms−1⇒0.08×10−2kgms−1
Therefore, the magnitude of impulse is 0.08×10−2kgms−1
25. Figure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with 1ms−21ms−2. What is the net force on the man? If the coefficient of static friction between the man’s shoes and the belt is 0.20.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt? (Mass of the man =65kg=65kg)

Ans: It is given that,
Mass of the man, m=65kgm=65kg
Acceleration of the belt, a=1ms−2a=1ms−2
Coefficient of static friction, μ=0.2μ=0.2
The net force FF, acting on the man is given by Newton’s second law of motion as: Fnet=maFnet=ma
⇒Fnet=65×1=65N⇒Fnet=65×1=65N
The man will continue to be stationary with respect to the convey or belt until the net force on the man is less than or equal to the frictional force fsfs exerted by the belt, i.e., F′net=fsF′net=fs
⇒ma′=μmg⇒ma′=μmg
⇒a′=0.2×10=2ms−2⇒a′=0.2×10=2ms−2
Therefore, the maximum acceleration of the belt up to which the man can stand stationary is a=2ms−2a=2ms−2.
26. A stone of mass mm tied to the end of a string revolves in a vertical circle of radius RR. The net forces at the lowest and highest points of the circle directed vertically downwards are: (Choose the correct alternative)
| Lowest Point | Highest point | |
|---|---|---|
| (a) | mg−T1 | mg+T2 |
| (b) | mg+T1 | mg−T2 |
| (c) | mg+T1−(mv21)R | mg−T2+(mv21)R |
| (d) | mg−T1−(mv21)R | mg+T2+(mv21)R |
T1T1 and v1v1 denote the tension and speed at the lowest point. T2T2 and v2v2 denote the tension and speed at the highest point.
Ans: (a)
The free body diagram of the stone at the lowest point is:
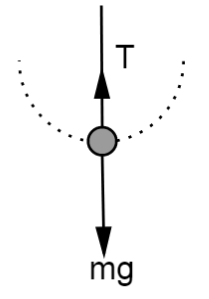
From Newton’s second law of motion,
The net force acting on the stone at this point is equal to the centripetal force: Fnet=T−mg=mv21R..........(1)Fnet=T−mg=mv12R..........(1)
Where, v1v1 is the velocity at the lowest point.
The free body diagram of the stone at the highest point is:
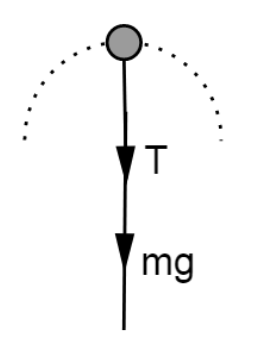
From Newton’s second law of motion: T+mg=mv22R.........(2)T+mg=mv22R.........(2)
Where, v2v2 is the velocity at the highest point.
From equations (1)(1) and (2)(2) the net force acting at the lowest and the highest points are (T−mg)(T−mg) and (T+mg)(T+mg) respectively.
27. A helicopter of mass 1000kg1000kgrises with a vertical acceleration of 15ms−215ms−2. The crew and the passengers weigh 300kg300kg. Give the magnitude and direction of the
a. force on the floor by the crew and passengers,
Ans: It is given that,
Mass of the helicopter, mh=1000kgmh=1000kg
Mass of the crew and passengers, mp=300kgmp=300kg
Total mass of the system, m=1300kgm=1300kg
Acceleration of the helicopter, a=15ms−2a=15ms−2
From Newton’s second law of motion,
The reaction force R, on the system by the floor is R−mpg=maR−mpg=ma
⇒R=mp(g+a)⇒R=mp(g+a)
⇒R=1300(10+15)=1300×25⇒R=1300(10+15)=1300×25
⇒R=7500N⇒R=7500N
As the helicopter is accelerating vertically upward, the reaction force will also be directed upward.
Hence, from Newton’s third law of motion, the force on the floor by the crew and passengers is 7500N7500N, directed downward.
b.action of the rotor of the helicopter on the surrounding air,
Ans: From Newton’s second law of motion,
The reaction force R′R′ experienced by the helicopter is: R′−mg=maR′−mg=ma
⇒R′=m(g+a)⇒R′=m(g+a)
⇒R′=1300(10+15)⇒R′=1300(10+15)
⇒R′=1300×25⇒R′=1300×25
⇒R′=32500N⇒R′=32500N
Hence, from Newton’s third law of motion, the action of the rotor on the surrounding air will be 32500N32500N, directed downward.
c. force on the helicopter due to the surrounding air.
Ans: The action of the rotor on the surrounding air is 32500N32500N, directed downward. Therefore, the reaction force experienced by the helicopter from the surrounding air is acting upward.
Thus, the force on the helicopter due to the surrounding air is32500N32500N, directed upward. .
28. A stream of water flowing horizontally with a speed of 15ms−115ms−1 gushes out of a tube of cross-sectional area 10−2m210−2m2 and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water, assuming it does not rebound?
Ans: It is given that,
Speed of the water stream, v=15m/sv=15m/s
Cross-sectional area of the tube, A=10−2m2A=10−2m2
Volume of water coming out from the pipe per second, V=Av=15×10−2m3/sV=Av=15×10−2m3/s
Density of water, ρ=103kg/m3ρ=103kg/m3
Mass of water flowing out through the pipe per second=ρ×V=150kg/s=ρ×V=150kg/s
The water strikes the wall and does not rebound.
Therefore, the force exerted by the water on the wall is given by Newton’s second law of motion as: F=ΔPΔtF=ΔPΔt M
Where, F=F= Rate of change of momentum per second
⇒F=mvt=150×151⇒F=mvt=150×151
⇒F=2250N⇒F=2250N
Therefore, the force exerted on the wall is 2250N2250N.
29. Ten one-rupee coins are put on top of each other on a table. Each coin has a mass mm. Give the magnitude and direction of
the force on the 7th7th coin (counted from the bottom) due to all the coins on its top,
Ans: It is given that,
Weight of one coin=mg=mg
Weight of three coins=3mg=3mg
Force on the seventh coin is exerted by the weight of the three coins on its top.
Therefore, the force exerted on the 7th7thcoin by the three coins on its top is 3mg3mg . This force acts vertically downward.
the force on the 7th7th coin by the eighth coin,
Ans: Force on the seventh coin by the eighth coin is because of the weight of the eighth coin and the other two coins (ninth and tenth) on its top.
Weight of the eighth coin=mg=mg
Weight of the ninth coin=mg=mg
Weight of the tenth coin=mg=mg
Total weight of these three coins=3mg=3mg
Therefore, the force exerted on the 7th7th coin by the eighth coin is 3mg3mg. This force acts vertically downward.
the reaction of the 6th6th coin on the 7th7th coin.
Ans: The 6th6th coin experiences a downward force because of the weight of the four coins (7th7th,8th8th,9th9th, and 10th10th) on its top.
Thus, the total downward force experienced by the 6th6th coin is 4mg4mg.
From Newton’s third law of motion,
The 6th6th coin will produce an equal reaction force on the 7th7th coin, but in the opposite direction.
Therefore, the reaction force of the 6th6th coin on the 7th7thcoin is of magnitude 4mg4mg. This force acts in the upward direction.
30. An aircraft executes a horizontal loop at a speed of 720km/h720km/h with its wings banked at 15∘15∘. What is the radius of the loop?
Ans: It is given that
Speed of the aircraft, v=720km/hv=720km/h
⇒v=720×518=200m/s⇒v=720×518=200m/s
Acceleration due to gravity, a=g=10ms−2a=g=10ms−2
Angle of banking, θ=15∘θ=15∘
Let rr be the radius of the loop.
It is known that the angle of banking is related to the radius (r)(r) and speed (v)(v) by the relation: tanθ=v2rgtanθ=v2rg
⇒r=v2gtanθ⇒r=v2gtanθ
⇒r=(200)210×tan15∘=40000.2679⇒r=(200)210×tan15∘=40000.2679
⇒r=14,928.2m⇒r=14,928.2m
Therefore, the radius of the loop is 14,928.2m
31. A train runs along an unbanked circular track of radius 30m30m at a speed of 54km/h 54km/h . The mass of the train is 106kg106kg . What provides the centripetal force required for this purpose -The engine or the rails? What is the angle of banking required to prevent wearing out of the rail?
Ans: It is given that,
Radius of the circular track, r=30mr=30m
Speed of the train, v=54 km/h=54×518=15m/s
v=54 km/h=54×518=15m/s
Mass of the train, m=106kgm=106kg
The centripetal force is provided by the lateral thrust of the rail on the wheel.
Therefore, from Newton’s third law of motion, the wheel exerts an equal and opposite force on the rail. This reaction force is responsible for the wear and rear of the rail.
It is known that the angle of banking is related to the radius (r)(r) and speed (v)(v) by the relation: tanθ=v2rgtanθ=v2rg
⇒tanθ=(15)230×10=225300⇒tanθ=(15)230×10=225300
⇒θ=tan−1(0.75)=36.87∘⇒θ=tan−1(0.75)=36.87∘
Therefore, the angle of banking required to prevent wearing out of the rail is 36.87∘
32. A block of mass 25kg25kg is raised by a 50kg50kg man in two different ways as shown in figure. What is the action on the floor by the man in the two cases? If the floor yields to a normal force of 700N700N, which mode should the man adopt to lift the block without the floor yielding?
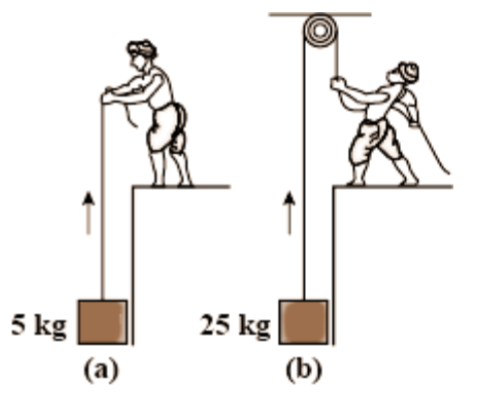
Ans: It is given that,
Mass of the man, M=50kgM=50kg
Acceleration due to gravity, g=10ms−2g=10ms−2
Force applied on the block, F=25×10=250N
F=25×10=250N
Weight of the man, W=50×10=500N
W=50×10=500N
Case (a)(a): When the man lifts the block directly
In this case, the man applies a force in the upward direction. This increases his apparent weight.
Action on the floor by the man =250+500=750N
=250+500=750N
Case (b)(b): When the man lifts the block using a pulley
In this case, the man applies a force in the downward direction. This decreases his apparent weight.
Action on the floor by the man=500250=250N
=500250=250N
If the floor can yield to a normal force of 700N700N, then the man should adopt the second method to easily lift the block by applying lesser force.
Therefore, case (b)(b) is adopted.
33. A monkey of mass 40kg40kg climbs on a rope (figure) which can stand a maximum tension of 600N600N. Ignore the mass of the rope. In which of the following cases will the rope break: the monkey

a.climbs up with an acceleration of 6ms−26ms−2
Ans: It is given that,
Mass of the monkey, m=40kgm=40kg m
Acceleration due to gravity, g=10ms−2g=10ms−2
Maximum tension that the rope can bear, Tmax=600NTmax=600N
Acceleration of the monkey, a=6m/s2a=6m/s2 upward
From Newton’s second law of motion:
It can be written: Tmg=ma
Tmg=ma
⇒T=m(a+g)
⇒T=m(a+g)
⇒T=40(6+10)
⇒T=40(6+10)
⇒T=40×16=640N
⇒T=40×16=640N
Therefore, as T>TmaxT>Tmax the rope will break.
b. climbs down with an acceleration of 4ms−24ms−2
Ans: Acceleration of the monkey, a=4m/s2a=4m/s2 downward
From Newton’s second law of motion: mg−T=mamg−T=ma
⇒T=m(g−a)⇒T=m(g−a)
⇒T=40(10−4)=240N⇒T=40(10−4)=240N
Therefore, as T
34. Two bodies A and B of masses 5kg5kg and 10kg10kg in contact with each other rest on a table against a rigid wall (figure). The coefficient of friction between the bodies and the table is 0.150.15. Ignore the difference between μsμs and μkμk.A force of 200N200Nis applied horizontally to A. What are
a.the reaction of the partition
Ans: It is given that,
Mass of body A, mA=5kgmA=5kg
Mass of body B, mB=10kgmB=10kg
Applied force, F=200NF=200N
Coefficient of friction, μs=0.15μs=0.15
The force of friction is: fs=μ(mA+mB)gfs=μ(mA+mB)g
⇒fs=0.15(5+10)×10⇒fs=0.15(5+10)×10
⇒fs=1.5×15=22.5N⇒fs=1.5×15=22.5N leftward
Net force acting on the partition =20022.5=177.5N
=20022.5=177.5N
rightward
From Newton’s third law of motion,
The reaction force of the partition will be in the direction opposite to the net applied force.
Therefore, the reaction of the partition will be 177.5N177.5N, in the leftward direction.
b. the action-reaction forces between A and B? What happens when the wall is removed? Does the answer to (b)(b) change, when the bodies are in motion?
Ans: Force of friction on mass AA : fA=μmAgfA=μmAg
⇒fA=0.15×5×10=7.5N⇒fA=0.15×5×10=7.5N leftward
Net force exerted by mass AA on mass BB =2007.5=192.5N
=2007.5=192.5N
rightward
From Newton’s third law of motion,
An equal amount of reaction force will be exerted by mass BB on mass AA, i.e., 192.5N
192.5N
acting leftward.
When the wall is removed, the two bodies will move in the direction of the applied force.
Net force acting on the moving system=177.5N=177.5N
The equation of motion for the system of acceleration aa,Net force=(mA+mB)aNet force=(mA+mB)a
⇒a=Net force(mA+mB)⇒a=Net force(mA+mB)
⇒a=177.5(5+10)=177.515=11.83ms−2⇒a=177.5(5+10)=177.515=11.83ms−2
Net force causing mass AA to move: FA=mAaFA=mAa
⇒FA=5×11.83=59.15N⇒FA=5×11.83=59.15N
Net force exerted by mass AA on mass BB=192.559.15=133.35N
=192.559.15=133.35N
This force will act in the direction of motion.
From Newton’s third law of motion, an equal amount of force will be exerted by mass BB on mass AA , i.e., 133.3N133.3N , acting opposite to the direction of motion.
35. A block of mass 15kg15kg is placed on a long trolley. The coefficient of static friction between the block and the trolley is 0.180.18. The trolley accelerates from rest with 0.5ms−20.5ms−2 for 20s20s and then moves with uniform velocity. Discuss the motion of the block as viewed by
a stationary observer on the ground,
Ans: It is given that,
Mass of the block, m=15kgm=15kg
Coefficient of static friction, μ=0.18μ=0.18
Acceleration of the trolley, a=0.5ms−2a=0.5ms−2
From Newton’s second law of motion,
The force (F)(F) on the block caused by the motion of the trolley is: F=maF=ma
⇒F=15×0.5=7.5N⇒F=15×0.5=7.5N
This force is acted in the direction of motion of the trolley.
Force of static friction between the block and the trolley
f=μmgf=μmg
f=0.18×15×10=27Nf=0.18×15×10=27
The force of static friction between the block and the trolley is greater than the applied external force.
Therefore, for an observer on the ground, the block will appear to be at rest.
When the trolley moves with uniform velocity there will be no applied external force. Only the force of friction will act on the block in this situation.
an observer moving with the trolley.
Ans: An observer, moving with the trolley, has some acceleration. This is the case of non-inertial frame of reference.
The frictional force, acting on the trolley backward, is opposed by a pseudo force of the same magnitude. However, this force acts in the opposite direction.
Therefore, the trolley will appear to be at rest for the observer moving with the trolley.
36. The rear side of a truck is open and a box of 40kg40kg mass is placed 5m5m away from the open end as shown in figure. The coefficient of friction between the box and the surface below it is 0.150.15. On a straight road, the truck starts from rest and accelerates with 2ms−22ms−2. At what distance from the starting point does the box fall off the truck? (Ignore the size of the box).
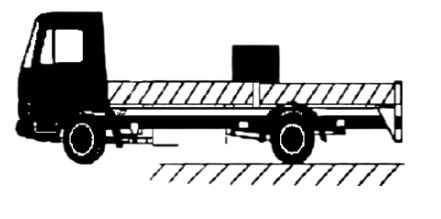
Ans: It is given that,
Mass of the box, m=40kgm=40kg
Coefficient of friction, μ=0.15μ=0.15
Initial velocity, u=0u=0
Acceleration, a=2m/s2a=2m/s2
Distance of the box from the end of the truck, s′=5ms′=5m
From Newton’s second law of motion,
The force on the box caused by the accelerated motion of the truck is: F=ma=2×40=80NF=ma=2×40=80N
From Newton’s third law of motion, a reaction force of 80N80N is acting on the box in the backward direction.
The backward motion of the box is opposed by the force of friction ff, acting between the box and the floor of the truck.
f=μmgf=μmg
⇒f=0.15×40×10=60N⇒f=0.15×40×10=60N
Net force acting on the block: Fnet=80−60=20NFnet=80−60=20N backward
The backward acceleration produced in the box is given by:
aback=Fnetm=2040=0.5ms−2aback=Fnetm=2040=0.5ms−2
From the second equation of motion, time tt can be calculated as:s′=ut+12abackt2s′=ut+12abackt2
⇒5=0+12×0.5×t2⇒5=0+12×0.5×t2
⇒t=20−−√s⇒t=20s
Therefore, the box will fall from the truck after 20−−√s20s from start.
The distance ss, travelled by the truck in 20−−√s20s is: s=ut+12at2s=ut+12at2
⇒s=0+12×2×(2–√)2⇒s=0+12×2×(2)2
⇒s=20m⇒s=20m
Therefore, at a distance of 20m20m from the starting point the box falls off the truck.
37. A disc revolves with a speed of 3313rev/min3313rev/min, and has a radius of 15cm15cm. Two coins are placed at 4cm4cm and 14cm14cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.150.15, which of the coins will revolve with the record?
Ans: It is given that,
Radius of the disc, r=15cm=0.15m
r=15cm=0.15m
Frequency of revolution, ν=3313rev/minν=3313rev/min
ν=1003×60=59rev/sν=1003×60=59rev/s M
Coefficient of friction, μ=0.15μ=0.15
Let, mass of each coin be mm.
In the given case, the coin having a force of friction greater than or equal to the centripetal force provided by the rotation of the disc will revolve with the disc.
If this is not the case, then the coin will slip from the disc.
When coin is placed at 4cm4cm:
Radius of revolution, r′=4cm=0.04mr′=4cm=0.04m
Angular frequency, ω=2πν=2×227×59=3.49s−1ω=2πν=2×227×59=3.49s−1
Frictional force, f=μmg=0.15×m×10=1.5mNf=μmg=0.15×m×10=1.5mN
Centripetal force on the coin: Fcent=mr′ω2Fcent=mr′ω2
⇒Fcent=m×0.04×(3.49)2⇒Fcent=m×0.04×(3.49)2
⇒Fcent=0.49mN⇒Fcent=0.49mN
Therefore, as f>Fcentf>Fcentthe coin will revolve along with the record.
When coin is placed at 14cm14cm:
Radius of revolution, r′′=14cm=0.14mr″=14cm=0.14m
Angular frequency, ω=2πν=2×227×59=3.49s−1ω=2πν=2×227×59=3.49s−1
Frictional force, f′=μmg=0.15×m×10=1.5mNf′=μmg=0.15×m×10=1.5mN
Centripetal force on the coin: Fcent=mr′′ω2Fcent=mr″ω2
⇒Fcent=m×0.14×(3.49)2⇒Fcent=m×0.14×(3.49)2
⇒Fcent=1.7mN⇒Fcent=1.7mN
Therefore, as f
38. You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25m25m?
Ans: In a death-well, a motorcyclist does not fall at the top point of a vertical loop because both the force of normal reaction and the weight of the motorcyclist act downward and are balanced by the centripetal force. This situation is shown in the following figure.

The net force acting on the motorcyclist is the sum of the normal force and the force due to gravity (Fg=mg)(Fg=mg).
The equation of motion for the centripetal acceleration acac, can be written as:
F=macF=mac
⇒FN+Fg=mac⇒FN+Fg=mac
⇒FN+mg=mv2r⇒FN+mg=mv2r
For vminvmin , FN=0FN=0
⇒0+mg=mv2r⇒0+mg=mv2r
⇒vmin=gr−−√⇒vmin=gr
It is given that,r=25mr=25m
⇒vmin=25×10−−−−−−√=15.8m/s⇒vmin=25×10=15.8m/s
Therefore, the minimum speed required is 15.8m/s15.8m/s.
39. A 70kg70kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3m3m rotating about its vertical axis with 200rev/min200rev/min. The coefficient of friction between the wall and his clothing is 0.150.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
Ans: It is given that,
Mass of the man, m=70kgm=70kg
Radius of the drum, r=3mr=3m
Coefficient of friction, μ=0.15μ=0.15
Frequency of rotation, ν=200rev/min=20060=103rev/sν=200rev/min=20060=103rev/s
The necessary centripetal force required for the rotation of the man is provided by the normal force (NF)(NF).
When the floor revolves, the man sticks to the wall of the drum.
Therefore, the weight of the man (mg)(mg) acting downward is balanced by the frictional force (f=μFN)(f=μFN) acting upward.
Thus, the man will not fall until:mg
⇒mg<μFN=μmrω2⇒mg<μFN=μmrω2
⇒g<μrω2⇒g<μrω2
⇒ω>gμr−−√⇒ω>gμr
The minimum angular speed is given as:
ωmin>gμr−−√ωmin>gμr
⇒ωmin=100.15×3−−−−−√=4.71rads−1⇒ωmin=100.15×3=4.71rads−1
Therefore, the minimum rotational speed of the cylinder is 4.71rads−14.71rads−1.
40. A thin circular loop of radius RR rotates about its vertical diameter with an angular frequency ωω. Show that a small bead on the wire loop remains at its lowermost point for ω≤gR−−√ω≤gR. What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=2gR−−√ω=2gR ? Neglect friction.
Ans.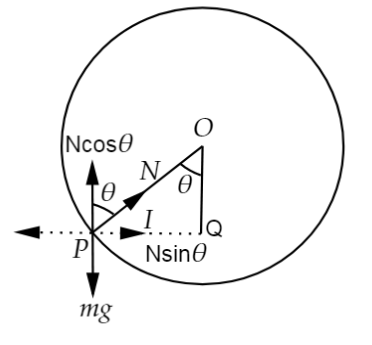
Let the radius vector joining the bead with the centre make an angle θθ, with the vertical downward direction.
OP=R=OP=R= Radius of the circle
N=N= Normal reaction
Respective vertical and horizontal equations of forces can be written as:
mg=Ncosθmg=Ncosθ .........(1)(1)
mlω2=Nsinθmlω2=Nsinθ .........(2)(2)
From ΔOPQΔOPQ:sinθ=lRsinθ=lR
⇒l=Rsinθ⇒l=Rsinθ .........(3)(3)
Substituting equation (3)(3) in equation (2)(2):
⇒m(Rsinθ)ω2=Nsinθ⇒m(Rsinθ)ω2=Nsinθ
⇒mRω2=N⇒mRω2=N .........(4)(4)
Substituting equation (4)(4) in equation (1)(1):
⇒mg=mRω2cosθ⇒mg=mRω2cosθ
⇒cosθ=gRω2⇒cosθ=gRω2 .........(5)(5)
It is known that, cosθ≤1cosθ≤1
The bead will remain at its lowermost point for gRω2≤1gRω2≤1
⇒ω≤gR−−√⇒ω≤gR
For ω=2gR−−√ω=2gR or ω2=2gRω2=2gR .........(6)(6)
Equating equation (5)(5) and equation (6)(6)
⇒2gR=gRcosθ⇒2gR=gRcosθ
⇒cosθ=12⇒cosθ=12
⇒θ=cos−1(0.5)=60∘⇒θ=cos−1(0.5)=60∘
Therefore, the angle made by the radius vector joining the centre to the bead with the vertical is 60∘60∘.
Last Updated on: Mar 20, 2024
34. Two bodies A and B of masses 5kg5kg and 10kg10kg in contact with each other rest on a table against a rigid wall (figure). The coefficient of friction between the bodies and the table is 0.150.15. Ignore the difference between μsμs and μkμk.A force of 200N200Nis applied horizontally to A. What are
a.the reaction of the partition
Ans: It is given that,
Mass of body A, mA=5kgmA=5kg
Mass of body B, mB=10kgmB=10kg
Applied force, F=200NF=200N
Coefficient of friction, μs=0.15μs=0.15
The force of friction is: fs=μ(mA+mB)gfs=μ(mA+mB)g
⇒fs=0.15(5+10)×10⇒fs=0.15(5+10)×10
⇒fs=1.5×15=22.5N⇒fs=1.5×15=22.5N leftward
Net force acting on the partition =20022.5=177.5N
=20022.5=177.5N
rightward
From Newton’s third law of motion,
The reaction force of the partition will be in the direction opposite to the net applied force.
Therefore, the reaction of the partition will be 177.5N177.5N, in the leftward direction.
b. the action-reaction forces between A and B? What happens when the wall is removed? Does the answer to (b)(b) change, when the bodies are in motion?
Ans: Force of friction on mass AA : fA=μmAgfA=μmAg
⇒fA=0.15×5×10=7.5N⇒fA=0.15×5×10=7.5N leftward
Net force exerted by mass AA on mass BB =2007.5=192.5N
=2007.5=192.5N
rightward
From Newton’s third law of motion,
An equal amount of reaction force will be exerted by mass BB on mass AA, i.e., 192.5N
192.5N
acting leftward.
When the wall is removed, the two bodies will move in the direction of the applied force.
Net force acting on the moving system=177.5N=177.5N
The equation of motion for the system of acceleration aa,Net force=(mA+mB)aNet force=(mA+mB)a
⇒a=Net force(mA+mB)⇒a=Net force(mA+mB)
⇒a=177.5(5+10)=177.515=11.83ms−2⇒a=177.5(5+10)=177.515=11.83ms−2
Net force causing mass AA to move: FA=mAaFA=mAa
⇒FA=5×11.83=59.15N⇒FA=5×11.83=59.15N
Net force exerted by mass AA on mass BB=192.559.15=133.35N
=192.559.15=133.35N
This force will act in the direction of motion.
From Newton’s third law of motion, an equal amount of force will be exerted by mass BB on mass AA , i.e., 133.3N133.3N , acting opposite to the direction of motion.
35. A block of mass 15kg15kg is placed on a long trolley. The coefficient of static friction between the block and the trolley is 0.180.18. The trolley accelerates from rest with 0.5ms−20.5ms−2 for 20s20s and then moves with uniform velocity. Discuss the motion of the block as viewed by
a stationary observer on the ground,
Ans: It is given that,
Mass of the block, m=15kgm=15kg
Coefficient of static friction, μ=0.18μ=0.18
Acceleration of the trolley, a=0.5ms−2a=0.5ms−2
From Newton’s second law of motion,
The force (F)(F) on the block caused by the motion of the trolley is: F=maF=ma
⇒F=15×0.5=7.5N⇒F=15×0.5=7.5N
This force is acted in the direction of motion of the trolley.
Force of static friction between the block and the trolley
f=μmgf=μmg
f=0.18×15×10=27Nf=0.18×15×10=27
The force of static friction between the block and the trolley is greater than the applied external force.
Therefore, for an observer on the ground, the block will appear to be at rest.
When the trolley moves with uniform velocity there will be no applied external force. Only the force of friction will act on the block in this situation.
an observer moving with the trolley.
Ans: An observer, moving with the trolley, has some acceleration. This is the case of non-inertial frame of reference.
The frictional force, acting on the trolley backward, is opposed by a pseudo force of the same magnitude. However, this force acts in the opposite direction.
Therefore, the trolley will appear to be at rest for the observer moving with the trolley.
36. The rear side of a truck is open and a box of 40kg40kg mass is placed 5m5m away from the open end as shown in figure. The coefficient of friction between the box and the surface below it is 0.150.15. On a straight road, the truck starts from rest and accelerates with 2ms−22ms−2. At what distance from the starting point does the box fall off the truck? (Ignore the size of the box).

Ans: It is given that,
Mass of the box, m=40kgm=40kg
Coefficient of friction, μ=0.15μ=0.15
Initial velocity, u=0u=0
Acceleration, a=2m/s2a=2m/s2
Distance of the box from the end of the truck, s′=5ms′=5m
From Newton’s second law of motion,
The force on the box caused by the accelerated motion of the truck is: F=ma=2×40=80NF=ma=2×40=80N
From Newton’s third law of motion, a reaction force of 80N80N is acting on the box in the backward direction.
The backward motion of the box is opposed by the force of friction ff, acting between the box and the floor of the truck.
f=μmgf=μmg
⇒f=0.15×40×10=60N⇒f=0.15×40×10=60N
Net force acting on the block: Fnet=80−60=20NFnet=80−60=20N backward
The backward acceleration produced in the box is given by:
aback=Fnetm=2040=0.5ms−2aback=Fnetm=2040=0.5ms−2
From the second equation of motion, time tt can be calculated as:s′=ut+12abackt2s′=ut+12abackt2
⇒5=0+12×0.5×t2⇒5=0+12×0.5×t2
⇒t=20−−√s⇒t=20s
Therefore, the box will fall from the truck after 20−−√s20s from start.
The distance ss, travelled by the truck in 20−−√s20s is: s=ut+12at2s=ut+12at2
⇒s=0+12×2×(2–√)2⇒s=0+12×2×(2)2
⇒s=20m⇒s=20m
Therefore, at a distance of 20m20m from the starting point the box falls off the truck.
37. A disc revolves with a speed of 3313rev/min3313rev/min, and has a radius of 15cm15cm. Two coins are placed at 4cm4cm and 14cm14cm away from the centre of the record. If the co-efficient of friction between the coins and the record is 0.150.15, which of the coins will revolve with the record?
Ans: It is given that,
Radius of the disc, r=15cm=0.15m
r=15cm=0.15m
Frequency of revolution, ν=3313rev/minν=3313rev/min
ν=1003×60=59rev/sν=1003×60=59rev/s M
Coefficient of friction, μ=0.15μ=0.15
Let, mass of each coin be mm.
In the given case, the coin having a force of friction greater than or equal to the centripetal force provided by the rotation of the disc will revolve with the disc.
If this is not the case, then the coin will slip from the disc.
When coin is placed at 4cm4cm:
Radius of revolution, r′=4cm=0.04mr′=4cm=0.04m
Angular frequency, ω=2πν=2×227×59=3.49s−1ω=2πν=2×227×59=3.49s−1
Frictional force, f=μmg=0.15×m×10=1.5mNf=μmg=0.15×m×10=1.5mN
Centripetal force on the coin: Fcent=mr′ω2Fcent=mr′ω2
⇒Fcent=m×0.04×(3.49)2⇒Fcent=m×0.04×(3.49)2
⇒Fcent=0.49mN⇒Fcent=0.49mN
Therefore, as f>Fcentf>Fcentthe coin will revolve along with the record.
When coin is placed at 14cm14cm:
Radius of revolution, r′′=14cm=0.14mr″=14cm=0.14m
Angular frequency, ω=2πν=2×227×59=3.49s−1ω=2πν=2×227×59=3.49s−1
Frictional force, f′=μmg=0.15×m×10=1.5mNf′=μmg=0.15×m×10=1.5mN
Centripetal force on the coin: Fcent=mr′′ω2Fcent=mr″ω2
⇒Fcent=m×0.14×(3.49)2⇒Fcent=m×0.14×(3.49)2
⇒Fcent=1.7mN⇒Fcent=1.7mN
Therefore, as f
38. You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25m25m?
Ans: In a death-well, a motorcyclist does not fall at the top point of a vertical loop because both the force of normal reaction and the weight of the motorcyclist act downward and are balanced by the centripetal force. This situation is shown in the following figure.

The net force acting on the motorcyclist is the sum of the normal force and the force due to gravity (Fg=mg)(Fg=mg).
The equation of motion for the centripetal acceleration acac, can be written as:
F=macF=mac
⇒FN+Fg=mac⇒FN+Fg=mac
⇒FN+mg=mv2r⇒FN+mg=mv2r
For vminvmin , FN=0FN=0
⇒0+mg=mv2r⇒0+mg=mv2r
⇒vmin=gr−−√⇒vmin=gr
It is given that,r=25mr=25m
⇒vmin=25×10−−−−−−√=15.8m/s⇒vmin=25×10=15.8m/s
Therefore, the minimum speed required is 15.8m/s15.8m/s.
39. A 70kg70kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3m3m rotating about its vertical axis with 200rev/min200rev/min. The coefficient of friction between the wall and his clothing is 0.150.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
Ans: It is given that,
Mass of the man, m=70kgm=70kg
Radius of the drum, r=3mr=3m
Coefficient of friction, μ=0.15μ=0.15
Frequency of rotation, ν=200rev/min=20060=103rev/sν=200rev/min=20060=103rev/s
The necessary centripetal force required for the rotation of the man is provided by the normal force (NF)(NF).
When the floor revolves, the man sticks to the wall of the drum.
Therefore, the weight of the man (mg)(mg) acting downward is balanced by the frictional force (f=μFN)(f=μFN) acting upward.
Thus, the man will not fall until:mg
⇒mg<μFN=μmrω2⇒mg<μFN=μmrω2
⇒g<μrω2⇒g<μrω2
⇒ω>gμr−−√⇒ω>gμr
The minimum angular speed is given as:
ωmin>gμr−−√ωmin>gμr
⇒ωmin=100.15×3−−−−−√=4.71rads−1⇒ωmin=100.15×3=4.71rads−1
Therefore, the minimum rotational speed of the cylinder is 4.71rads−14.71rads−1.
40. A thin circular loop of radius RR rotates about its vertical diameter with an angular frequency ωω. Show that a small bead on the wire loop remains at its lowermost point for ω≤gR−−√ω≤gR. What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=2gR−−√ω=2gR ? Neglect friction.
Ans.
Let the radius vector joining the bead with the centre make an angle θθ, with the vertical downward direction.
OP=R=OP=R= Radius of the circle
N=N= Normal reaction
Respective vertical and horizontal equations of forces can be written as:
mg=Ncosθmg=Ncosθ .........(1)(1)
mlω2=Nsinθmlω2=Nsinθ .........(2)(2)
From ΔOPQΔOPQ:sinθ=lRsinθ=lR
⇒l=Rsinθ⇒l=Rsinθ .........(3)(3)
Substituting equation (3)(3) in equation (2)(2):
⇒m(Rsinθ)ω2=Nsinθ⇒m(Rsinθ)ω2=Nsinθ
⇒mRω2=N⇒mRω2=N .........(4)(4)
Substituting equation (4)(4) in equation (1)(1):
⇒mg=mRω2cosθ⇒mg=mRω2cosθ
⇒cosθ=gRω2⇒cosθ=gRω2 .........(5)(5)
It is known that, cosθ≤1cosθ≤1
The bead will remain at its lowermost point for gRω2≤1gRω2≤1
⇒ω≤gR−−√⇒ω≤gR
For ω=2gR−−√ω=2gR or ω2=2gRω2=2gR .........(6)(6)
Equating equation (5)(5) and equation (6)(6)
⇒2gR=gRcosθ⇒2gR=gRcosθ
⇒cosθ=12⇒cosθ=12
⇒θ=cos−1(0.5)=60∘⇒θ=cos−1(0.5)=60∘
Therefore, the angle made by the radius vector joining the centre to the bead with the vertical is 60∘60∘.
Last Updated on: Mar 20, 2024
38. You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘death-well’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25m25m?
Ans: In a death-well, a motorcyclist does not fall at the top point of a vertical loop because both the force of normal reaction and the weight of the motorcyclist act downward and are balanced by the centripetal force. This situation is shown in the following figure.

The net force acting on the motorcyclist is the sum of the normal force and the force due to gravity (Fg=mg)(Fg=mg).
The equation of motion for the centripetal acceleration acac, can be written as:
F=macF=mac
⇒FN+Fg=mac⇒FN+Fg=mac
⇒FN+mg=mv2r⇒FN+mg=mv2r
For vminvmin , FN=0FN=0
⇒0+mg=mv2r⇒0+mg=mv2r
⇒vmin=gr−−√⇒vmin=gr
It is given that,r=25mr=25m
⇒vmin=25×10−−−−−−√=15.8m/s⇒vmin=25×10=15.8m/s
Therefore, the minimum speed required is 15.8m/s15.8m/s.
39. A 70kg70kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3m3m rotating about its vertical axis with 200rev/min200rev/min. The coefficient of friction between the wall and his clothing is 0.150.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
Ans: It is given that,
Mass of the man, m=70kgm=70kg
Radius of the drum, r=3mr=3m
Coefficient of friction, μ=0.15μ=0.15
Frequency of rotation, ν=200rev/min=20060=103rev/sν=200rev/min=20060=103rev/s
The necessary centripetal force required for the rotation of the man is provided by the normal force (NF)(NF).
When the floor revolves, the man sticks to the wall of the drum.
Therefore, the weight of the man (mg)(mg) acting downward is balanced by the frictional force (f=μFN)(f=μFN) acting upward.
Thus, the man will not fall until:mg
⇒mg<μFN=μmrω2⇒mg<μFN=μmrω2
⇒g<μrω2⇒g<μrω2
⇒ω>gμr−−√⇒ω>gμr
The minimum angular speed is given as:
ωmin>gμr−−√ωmin>gμr
⇒ωmin=100.15×3−−−−−√=4.71rads−1⇒ωmin=100.15×3=4.71rads−1
Therefore, the minimum rotational speed of the cylinder is 4.71rads−14.71rads−1.
⇒g<μrω2⇒g<μrω2
⇒ω>gμr−−√⇒ω>gμr
The minimum angular speed is given as:
ωmin>gμr−−√ωmin>gμr
⇒ωmin=100.15×3−−−−−√=4.71rads−1⇒ωmin=100.15×3=4.71rads−1
Therefore, the minimum rotational speed of the cylinder is 4.71rads−14.71rads−1.
40. A thin circular loop of radius RR rotates about its vertical diameter with an angular frequency ωω. Show that a small bead on the wire loop remains at its lowermost point for ω≤gR−−√ω≤gR. What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=2gR−−√ω=2gR ? Neglect friction.
Ans.
Let the radius vector joining the bead with the centre make an angle θθ, with the vertical downward direction.
OP=R=OP=R= Radius of the circle
N=N= Normal reaction
Respective vertical and horizontal equations of forces can be written as:
mg=Ncosθmg=Ncosθ .........(1)(1)
mlω2=Nsinθmlω2=Nsinθ .........(2)(2)
From ΔOPQΔOPQ:sinθ=lRsinθ=lR
⇒l=Rsinθ⇒l=Rsinθ .........(3)(3)
Substituting equation (3)(3) in equation (2)(2):
⇒m(Rsinθ)ω2=Nsinθ⇒m(Rsinθ)ω2=Nsinθ
⇒mRω2=N⇒mRω2=N .........(4)(4)
Substituting equation (4)(4) in equation (1)(1):
⇒mg=mRω2cosθ⇒mg=mRω2cosθ
⇒cosθ=gRω2⇒cosθ=gRω2 .........(5)(5)
It is known that, cosθ≤1cosθ≤1
The bead will remain at its lowermost point for gRω2≤1gRω2≤1
⇒ω≤gR−−√⇒ω≤gR
For ω=2gR−−√ω=2gR or ω2=2gRω2=2gR .........(6)(6)
Equating equation (5)(5) and equation (6)(6)
⇒2gR=gRcosθ⇒2gR=gRcosθ
⇒cosθ=12⇒cosθ=12
⇒θ=cos−1(0.5)=60∘⇒θ=cos−1(0.5)=60∘
Therefore, the angle made by the radius vector joining the centre to the bead with the vertical is 60∘60∘.
Last Updated on: Mar 20, 2024
