Chapter 9 Mechanical Properties of Solids Questions and Answers: NCERT Solutions for Class 11th Physics (Partnership Physics )

CBSE 10th Date sheet 2022      CBSE 12th Date Sheet 2022

Class 11th Physics (Partnership Physics ) NCERT book solutions for Chapter 9 Mechanical Properties of Solids Questions and Answers.

---

1. A steel wire of length 4.7 m and cross-sectional area 3.0×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area 4.0×10−5m2 of under a given load. What is the ratio of the Young’s modulus of steel to that of copper?

Ans: In the above question it is given that:
The length of the steel wire is L1=4.7m.
Area of cross-section of the steel wire is A1=3.0×10−5m2
The length of the copper wire is L2=3.5m.
Area of cross-section of the copper wire is A2=4.0×10−5m2
Now,
The change in length is given by:
ΔL=L1−L2=4.7−3.5=1.2m
Let the force applied in both the cases be F .
Therefore, Young’s modulus of the steel wire is given by:
Y1=FA1×L1ΔL=F×4.73.0×10−5×1.2 …… (1)
And Young’s modulus of the copper wire is given by:
Y2=FA2×L2ΔL=F×3.54.0×10−5×1.2 …… (2)
Therefore,
Y1Y2=F×4.7×4.0×10−5×1.23.0×10−5×1.2×F×3.5=1.791
Hence the ratio of Young’s modulus of steel to that of copper is 1.79:1

---

2. Figure shows the strain-stress curve for a given material. What are a) Young’s modulus?

b) Approximate yield strength for this material?

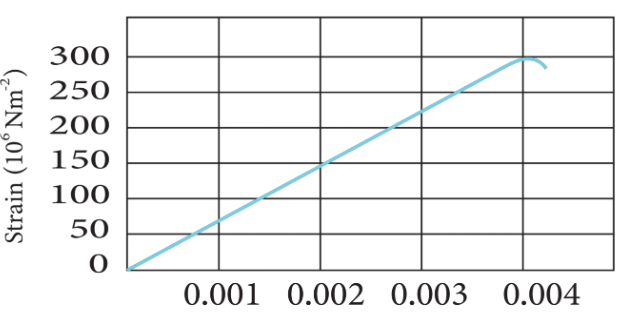
Ans: From the graph given in the above question it is clear that:
Stress for a given material is 150×106N/m2 and strain is 0.002.
Young’s modulus is given by:
Y=StressStrain
⇒Y=150×106N/m20.002=7.5×1010N/m2
Therefore, Young’s modulus for the given material is

---

3. The stress-strain graphs for materials A and B are shown in figure.

The graphs are drawn to the same scale.
a) Which of the materials has the greater Young’s modulus?

Ans: In the two graphs it is that given that stress for A is more than that of B.
As,
Young′s modulus=StressStrain
Therefore, material A has greater Young's modulus.
b) Which of the two is the stronger material?
Ans: The strength of a material is determined by the amount of stress required for fracturing a material, corresponding to its fracture point.
Fracture point is defined as the extreme point in a stress-strain curve.
From the graph it is clear that material A can withstand more strain than material B.
Therefore, material A is stronger than material B.

---

4. Read the following two statements below carefully and state, with reasons, if it is true or false. a) The Young’s modulus of rubber is greater than that of steel.

Ans: The given statement is false.
As there is more strain in rubber than steel and modulus of elasticity is inversely proportional to strain. Therefore, the Young’s modulus of steel is greater than that of rubber.
b) The stretching of a coil is determined by its shear modulus.
Ans: The given statement is true.
As the shear modulus of a coil relates with the change in shape of the coil and the stretching of coil changes its shape without any change in the length. Therefore, the shear modulus of elasticity is involved. Hence the stretching of a coil is determined by its shear modulus.

---

5. Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.

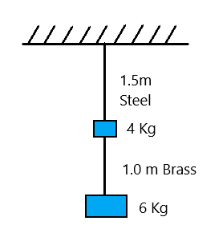
Ans: In the above question it is given that:
Diameter of the wires is d=0.25m.
Hence r=0.125m.
Length of the steel wire is L1=1.5m.
Length of the brass wire is L2=1.0m.
Total force exerted on the steel wire is F1=(4+6)g=10g
∴F1=10×9.8=98N.
Young’s modulus for steel is given by
Y1=F1A1×L1ΔL1
Where,
ΔL1 is the change in the length of the steel wire.
And A1 is the area of cross-section of the steel wire.
∴A1=πr12
We have,
Young’s modulus of steel is Y1=2.0×1011Pa.
⇒ΔL1=F1×L1A1×Y1
⇒ΔL1=98×1.5π(0.125)2×2.0×1011=1.49×10−4m.
Total force on the brass wire is F2=6×9.8=58.8N.
Young’s modulus for brass is given by
Y2=F2A2×L2ΔL2
Where,
ΔL2 is the change in the length of the brass wire.
And A2 is the area of cross-section of the brass wire.
∴A2=πr22
We have,
Young’s modulus of brass is Y2=0.91×1011Pa.
⇒ΔL2=F2×L2A2×Y2
⇒ΔL2=58.8×1π(0.125)2×0.91×1011=1.3×10−4m.
Clearly, the elongation of the steel wire is 1.49×10−4m and that of the brass wire is 1.3×10−4m.

---

6. The edge of an aluminium cube is 10 cm long. One face of the cube is firmly fixed to a vertical wall. A mass of 100 kg is then attached to the opposite face of the cube. The shear modulus of aluminium is 25 GPa. What is the vertical deflection of this face?

Ans: In the above question it is given that:
Edge of the aluminium cube is L=10cm=0.1m.
The mass attached to the cube is m=100kg.
Shear modulus η of aluminium is 25GPa=25×1010Pa.
We know that:
Shear modulus(η)=Shear stressShear strain
⇒η=(FA)(LΔL)
Where,
F is the applied force.
∴F=mg=100×9.8=980N
Area of one of the faces of the cube is A=0.1×0.1=0.01m2.
Vertical deflection of the cube is ΔL.
ΔL=FLAη
⇒ΔL=980×0.10.01×25×109=3.92×10−7m
Clearly, the vertical deflection of this face of the cube is 3.92×10−7m.

---

7. Four identical hollow cylindrical columns of mild steel support a big structure of mass 50,000 kg. The inner and outer radii of each column are 30 cm and 60 cm respectively. Assuming the load distribution to be uniform, calculate the compressional strain of each column.

Ans: In the above question it is given that:
Mass of the big structure is M=50000kg.
Inner radius of the column is r=30cm=0.3m.
Outer radius of the column is R=60cm=0.6m
Young’s modulus of steel is Y=2×1011Pa
The total force exerted is F=Mg=50000×9.8N.
Stress = Force exerted on a single column
⇒Stress=50000×9.84=122500N
Young’s modulus is given by:
Y=StressStrain
⇒Strain=(FA)Y
Where,
Area is given by
A=π(R2−r2)=π((0.6)2−(0.3)2) .
⇒Strain=(50000×9.8π((0.6)2−(0.3)2))2×1011=7.22×10−7
Therefore, the compressional strain of each column is 7.22×10−7..

---

8. A piece of copper having a rectangular cross-section of 15.2 mm × 19.1 mm is pulled in tension with 44,500 N force, producing only elastic deformation. Calculate the resulting strain?

Ans: In the above question it is given that:
Length of the piece of copper is l=19.1mm=19.1×10−3m.
Breadth of the piece of copper is b=15.2mm=15.2×10−3m
Area of the copper piece will be:
A=l×b
⇒A=19.1×10−3×15.2×10−3=2.9×10−4m2
Tension force applied on the piece of copper is F=44500N.
Modulus of elasticity of copper is η=42×109N/m2.
We know that :
Modulus of elasticity(η)=StressStrain
⇒η=(FA)Strain
⇒Strain=FAη
⇒Strain=445002.9×10−4×42×109=3.65×10−3
Hence, the resulting strain is 3.65×10−3.

---

9. A steel cable with a radius of 1.5 cm supports a chairlift at a ski area. If the maximum stress is not to exceed 108N/m2, what is the maximum load the cable can support

Ans: In the above question it is given that:
Radius of the steel cable is r=1.5cm=0.015m.
Maximum allowable stress is 108N/m2.
We know that:
Maximum force = Maximum stress ×Area of cross-section
⇒Maximum force =108×π(0.015)2=7.065×104N
Therefore, the cable can support the maximum load of 7.065×104N

---

10. A rigid bar of mass 15 kg is supported symmetrically by three wires each 2.0 m long. Those at each end are of copper and the middle one is of iron. Determine the ratio of their diameters if each is to have the same tension.

Ans: In the above question it is given that:
Tension force acting on each wire is the same.
Therefore the extension produced in each wire is the same.
As the length of both wires is the same, the strain in both wires is also the same.
Young’s modulus is given by:
Y=StressStrain
⇒Y=(FA)Strain=4Fπd2Strain …… (1)
Where,
F is the Tension force,
A is the area of cross-section and
d is the diameter of the wire
From equation (1), it is clear that Y∝1d2.
Young’s modulus for iron is Y1=190×109Pa.
Let the diameter of the iron wire be d1.
Young’s modulus for copper is Y2=100×109Pa.
Let the diameter of the copper wire be d2.
Therefore, the ratio of their diameters is given as:
d2d1=Y1Y2−−√=190×109100×109−−−−−−√=1.311
Therefore, the ratio of diameters of copper wire to iron wire is 1.31:1

---

11. A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1.0 m, is whirled in a vertical circle with an angular velocity of 2 rev/s at the bottom of the circle. The cross-sectional area of the wire is 0.065cm2 . Calculate the elongation of the wire when the mass is at the lowest point of its path.

Ans: In the above question it is given that:
Mass is m=14.5 kg
. Length of the steel wire is l=1.0 m
Angular velocity is ω=2rev/s
Cross-sectional area of the wire is a=0.065cm2=0.065×10−4m2
Consider the elongation of the wire when the mass is at the lowest point of its path to be Δl.
The total force on the mass when the mass is placed at the position of the vertical circle is given by:
F=mg+mlω2
⇒F=14.5×9.8+14.5×1×24=200.1N
Young’s modulus is given by:
Y=StressStrain
⇒Y=(FA)(Δll)
⇒Δl=FlAY
We know that Young’s modulus for steel is 2×1011Pa.
Therefore,
Δl=220.1×10.065×10−4×2×1011=1.53×10−4m
Thus, the elongation of the wire is 1.53×10−4m

---

12. Compute the bulk modulus of water from the following data: Initial volume = 100.0 litre, Pressure increase = 100.0 atm(1atm=1.013×105Pa). Final volume = 100.5 litre. Compare the bulk modulus of water with that of air (at constant temperature). Explain in simple terms why the ratio is so large.

Ans: In the above question it is given that:
Initial volume is V1=100.0l=100×10−3m3.
Final volume is V2=100.5l=100.5×10−3m3.
Thus, the increase in volume is V2−V1=0.5×10−3m3.
Increase in pressure is Δp=100atm=100×1.013×105Pa.
The formula for bulk modulus is
Bulk Modulus=Δp(ΔVV1)=ΔpV1ΔV
⇒Bulk Modulus=100×1.013×105×100×10−30.5×10−3m3=2.026×109Pa
We know that Bulk modulus of air is 1×105Pa.
⇒Bulk modulus of waterBulk modulus of air=2.026×1091×105=2.026×104
This ratio is very high because air is more compressible than water

---

13. What is the density of water at a depth where pressure is 80.0 atm, given that its density at the surface is 1.03×103kg/m3

Ans: In the above question it is given that:
Pressure at the given depth is p=80.0atm=80×1.01×105Pa.
Consider the given depth to be h.
Density of water at the surface is ρ1=1.03×103kg/m3
Consider ρ2 to be the density of water at the depth h.
Consider V1 to be the volume of water of mass m at the surface.
Consider V2 to be the volume of water of mass m at the depth h.
Consider ΔV to be the change in volume.
ΔV=V1−V2
⇒ΔV=m[(1ρ1)−(1ρ2)]
Now,
Volumetric strain=m[(1ρ1)−(1ρ2)]×(ρ1m)
⇒ΔVV1=1−(ρ1ρ2) …… (1)
Bulk modulus is given by:
Bulk modulus=pV1ΔV
⇒ΔVV1=pB
Compressibility of water is given by:
1B=45.8×10−11Pa−1
⇒ΔVV1=80×1.013×105×45.8×10−11=3.71×10−3 …… (2)
From equations (1) and (2) we get:
1−(ρ1ρ2)=3.71×10−3
⇒ρ2=1.03×103[1−(3.71×10−3)]=1.034×103kgm−3
Clearly, the density of water at the given depth (h) is 1.034×103kgm−3

---

14. Compute the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm.

Ans: In the above question it is given that:
The hydraulic pressure exerted on the glass slab is p=10atm=10×1.013×105Pa.
Also, we know that the bulk modulus of glass is B=37×109N/m2.
Bulk modulus is given by the relation:
B=p(ΔVV)
Where,
ΔVV

is the fractional change in volume.
⇒(ΔVV)=pB
⇒(ΔVV)=10×1.013×10537×109=2.73×10−5
Clearly, the fractional change in the volume of the glass slab is 2.73×10−5

---

15. Determine the volume contraction of a solid copper cube, 10 cm on an edge, when subjected to a hydraulic pressure of 7×106Pa.

Ans: In the above question it is given that:
The length of an edge of the solid copper cube is l=10cm=0.1m.
Hydraulic pressure is p=7×106Pa.
Bulk modulus of copper is B=140×109Pa.
Bulk modulus is given by the relation:
B=p(ΔVV)
Where,
ΔVV
is the volumetric strain
ΔV is the change in volume.
V is the original volume.
⇒ΔV=pVB
The original volume of the cube is V=l3.
⇒ΔV=pl3B
⇒ΔV=7×106×(0.1)3140×109=5×10−8m3=5×10−2cm3
Clearly, the volume contraction of the solid copper cube is 5×10−2cm3

---

16. How much should the pressure on a litre of water be changed to compress it by 0.10%?

Ans: In the above question it is given that:
Volume of water is V=1L.
The water is to be compressed by 0.10
∴Fractional change=ΔVV=0.1100×1=10−3
Bulk modulus is given by the relation:
B=p(ΔVV)
⇒p=B×(ΔVV)
We know that, bulk modulus of water is B=2.2×109N/m2
⇒p=2.2×109×10−3=2.2×106N/m2
Clearly, the pressure on water should be 2.2×106N/m2

---

17. Anvils made of single crystals of diamond, with the shape as shown in figure, are used to investigate behaviour of materials under very high pressures. Flat faces at the narrow end of the anvil have a diameter of 0.50 mm, and the wide ends are subjected to a compressional force of 50,000 N. What is the pressure at the tip of the anvil?

Ans: In the above question it is given that:
The diameter of the cones at the narrow ends is d=0.50mm=0.5×10−3m
∴Radius will be r=0.25×10−3m
The Compressional force is F=50000N
Pressure at the tip of the anvil is given by:
P = ForceArea=50000π(0.25×10−3)2=2.55×1011Pa
Clearly, the pressure at the tip of the anvil will be 2.55×1011Pa

---

18. A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Fig. 9.15. The cross-sectional areas of wires A and B are 1.0mm2 and 2.0mm2, respectively. At what point along the rod should a mass m be suspended in order to produce a) Equal stresses

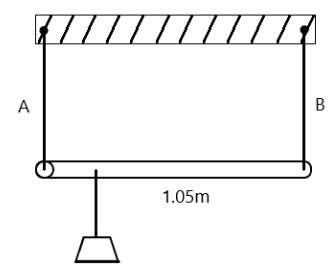
Ans: In the above question it is given that:
The cross-sectional area of wire A is 1.0mm2=1.0×10−6m2.
Cross-sectional area of wire B is 2.0mm2=2.0×10−6m2.
Young’s modulus for steel is Y1=2×1011N/m2 .
Young’s modulus for aluminium is Y2=7×1010N/m2.
Consider a small mass m to be suspended to the rod at a distance y from the end where wire A is attached.
Stress in the wire=Fa
If the two wires have equal stresses,
F1a1=F2a2
Where,
F1 is the force exerted on the steel wire.
F2 is the force exerted on the aluminium wire.
∴F1a1=F2a2=12 …… (1)
Consider the figure given below:

Taking torque about the point of suspension, we get: F1y=F2(1.05−y) …… (2)
From equations (1) and (2), we get:
(1.05−y)=12
⇒2(1.05−y)=y
⇒y=0.7m
Clearly, to produce an equal stress in the two wires, the mass must be suspended at a distance of 0.7m from the end where wire A is attached.
b) Equal strains in both steel and aluminium wires.
Ans: Young’s modulus is given by:
Y=StressStrain
⇒Strain=StressY=(Fa)Y
When the strain in the two wires is equal,
(F1a1)Y1=(F2a2)Y2
⇒F1F2=a1Y1a2Y2
We have
a1a2=12
⇒F1F2=1×2×10112×7×1010=107 …… (3)
Consider the torques about the point where mass m, to be suspended at a distance y1 from the side where wire A attached;
F1y1=F2(1.05−y1)
⇒F1F2=(1.05−y1)y1 …… (4)
From equations (3) and (4), we get:
(1.05−y1)=107
⇒7(1.05−y1)=10y1
⇒y1=0.432m
Clearly, to produce an equal strain in the two wires, the mass must be suspended at a distance of 0.432mfrom the end where wire A is attached

---

19. A mild steel wire of length 1.0 m and cross-sectional area 0.50×10−2cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.

Ans: In the above question it is given that:
Mass is m=100 g=0.100 kg
Length of the mild steel wire is 1.0m.
Cross-sectional area is 0.50×10−2cm2.
Now consider the figure given below:

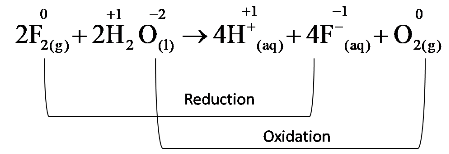
If x is the depression at the midpoint i.e., CD=x.
AB=BC=l=0.5m
AD=BD=l2+x2−−−−−−√
The increase in length will be:
Δl=AD+BD−AB=2AD−AB
⇒Δl=2l2+x2−−−−−−√−2l
⇒Δl=2l(1+x22l2)−2l
⇒Δl=2l(1+x22l2−1)=x2l
Now, we know that
Strain=increase in lengthoriginal length=x22l2
If T is the tension in the wire, then
2Tcosθ=mg
⇒T=mg2cosθ→(1)
Here,
cosθ=x(l2+x2)12=xl(1+x2l2)12=xl(1+x22l2)
As x< 1+x22l2≈1
⇒cosθ=xl→(2)
From (1) and (2),
T=mgl2x
Also, stress is given by:
Stress=TA=mgl2Ax
And Young’s modulus is given by:
Y=StressStrain
⇒Y=mgl2Ax×2l2x2=mgl3Ax3
⇒x=l(mgAY)13
⇒x=0.5[0.1×1020×1011×0.5×10−6]13=0.01074m
Clearly, the depression at the midpoint is 0.01074m .

---

20. Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9×107Pa ? Assume that each rivet is to carry one quarter of the load.

Ans: In the above question it is given that:
The diameter of the metal strip is d=6.0mm=6.0×10−3m.
Radius will be r=3.0×10−3m.
Maximum shearing stress is 6.9×107Pa.
We know that:
Maximum stress = Maximum load or forceArea
⇒Maximum force = Maximum stress × Area
⇒Maximum force = 6.9×107×π(r)2
⇒Maximum force = 6.9×107×π(3.0×10−3)2=1949.94N
Since each rivet is said to carry one quarter of the load;
Maximum tension on each rivet is 1949.94×4=7799.76N
Clearly, the maximum tension that can be exerted is 7799.76N

---

21. The Marina trench is located in the Pacific Ocean, and at one place it is nearly eleven km beneath the surface of water. The water pressure at the bottom of the trench is about 1.1×108Pa . A steel ball of initial volume is 0.32m3 dropped into the ocean and falls to the bottom of the trench. What is the change in the volume of the ball when it reaches the bottom?

Ans: In the above question it is given that:
Water pressure at the bottom of the trench is about 1.1×108Pa.
Initial volume of the steel ball is V=0.32m3.
Bulk modulus of steel is 1.6×1011N/m2.
The ball is said to fall at the bottom of the Pacific Ocean, which is 11 km beneath the surface.
Consider the change in the volume of the ball on reaching the bottom of the trench to be ΔV.
Bulk modulus is given by the relation:
B=p(ΔVV)
⇒ΔV=pVB
⇒ΔV=1.1×108×0.321.6×1011=2.2×10−4m3
Clearly, the change in volume of the ball on reaching the bottom of the trench is 2.2×10−4m3

---

Last Updated on: November 23, 2022