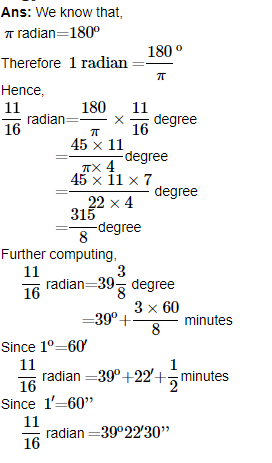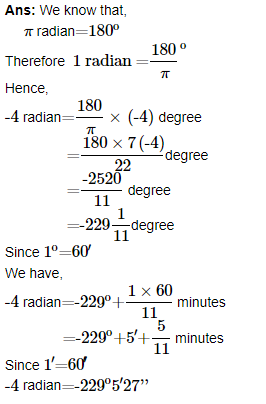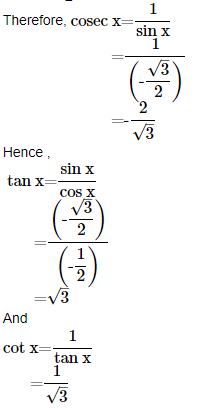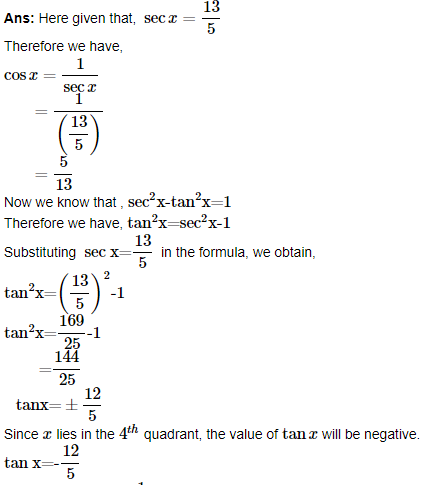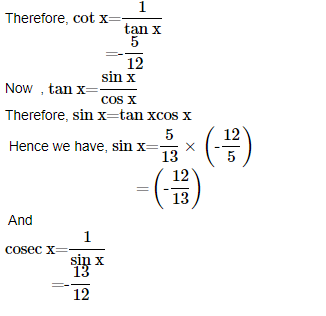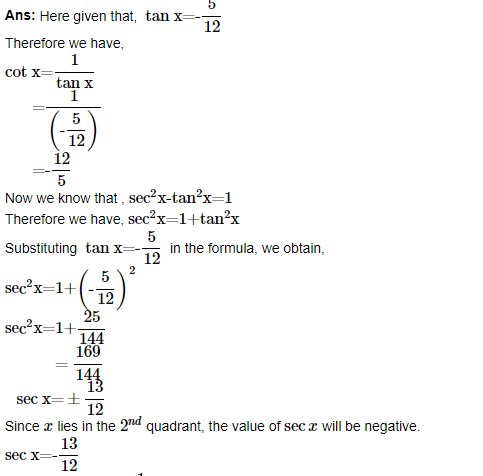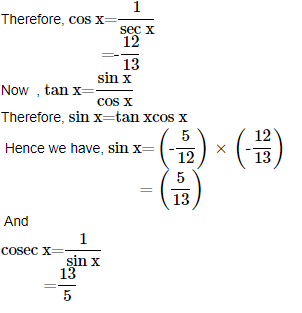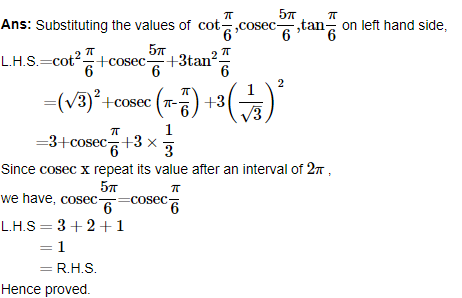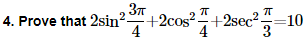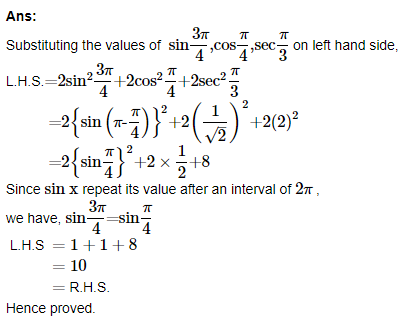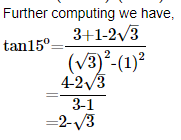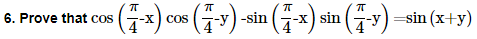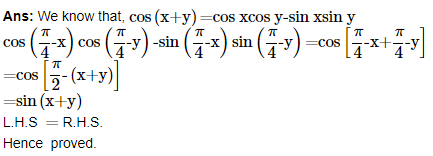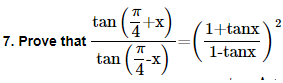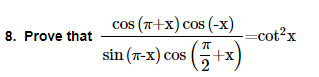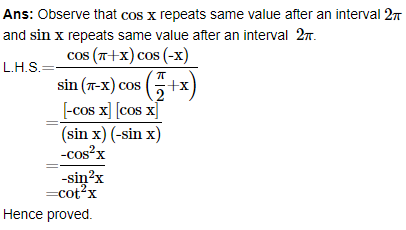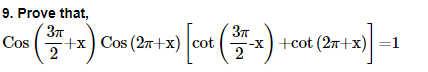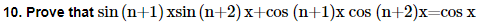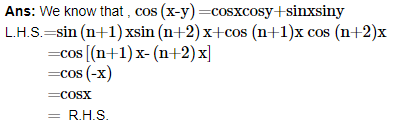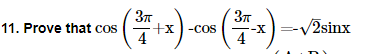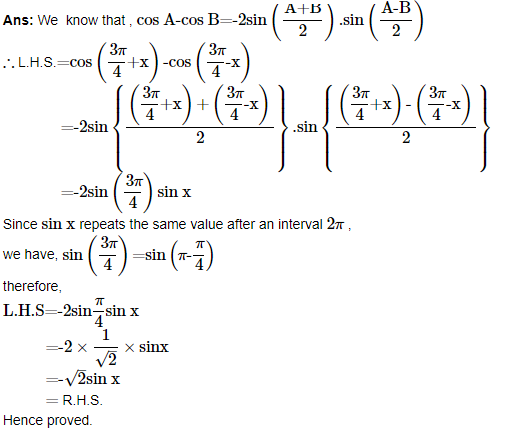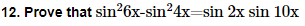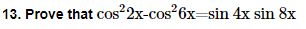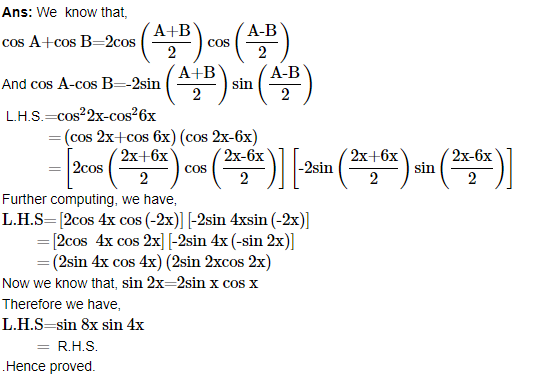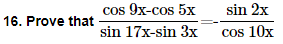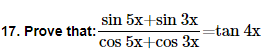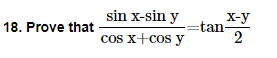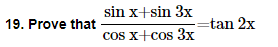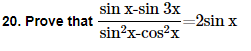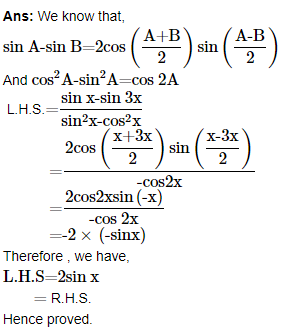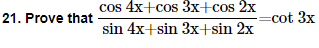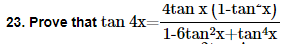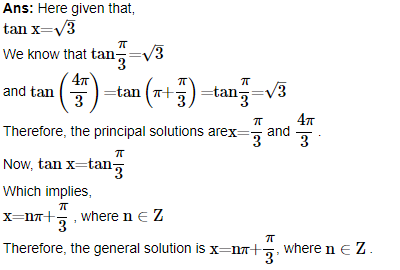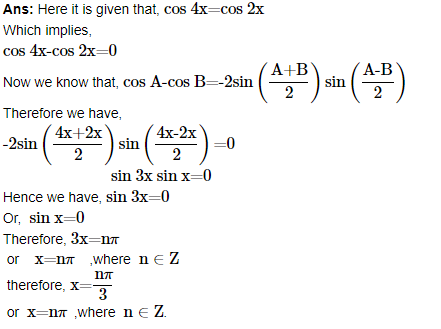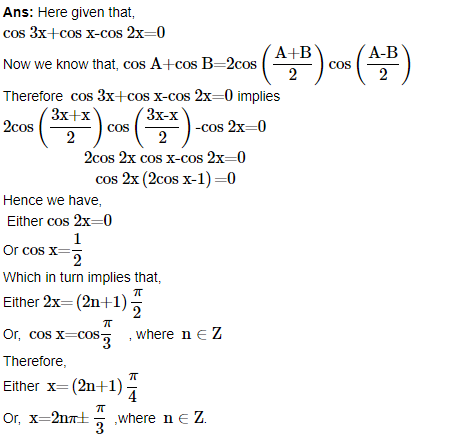Importance of Education

Education In India

MBA Colleges in India

Engineering Colleges in India

Universities and Colleges

Delhi University Colleges

How To Prepare For Exams

BBA Colleges in India

Medical Colleges in India

Hotel Management Colleges in India

MCA Colleges in India

BCA Colleges in India

B.Ed Colleges in India

Universities in India

chapter 3 trigonometric functions Questions and Answers: NCERT Solutions for Class 11th Maths

CBSE 10th Date sheet 2024 CBSE 12th Date Sheet 2024

Exercise 3.1

1. Find the radian measures corresponding to the following degree measures:

(i) 25o

(ii) -47o30 ′

(iii) 240o

(iv) 520o

2. Find the degree measures corresponding to the following radian measures (Use π =22/7 )

(i) 11/16

(ii) -4

(iii) 5π/3

(iv)7π/6

3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

Ans: Number of revolutions the wheel makes in 1 minute=360 Number of revolutions the wheel make in 1 second=360/60 =6 In one complete revolution, the wheel turns an angle of 2 π radian. Hence, it will turn an angle of 6 × 2 π =12 π radian, in 6 complete revolutions. Therefore, the wheel turns an angle of 12 π radian in one second.

4. Find the degree measure of the angle subtended at the centre of a circle of radius 100cm by an arc of length 22 cm.

6. If in two circles, arcs of the same length subtend angles 60o and 75o at the centre, find the ratio of their radii.

Ans: Let the radii of the two circles be r1 and r2 . Let an arc of length l1 subtends an angle of 60o at the centre of the circle of radius r1 , whereas let an arc of length l2 subtends an angle of 75o at the centre of the circle of radius r2 . Now, we have,

7. Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length.

(i) 10 cm

Ans: We know that, in a circle of radius r unit, if an angle θ radian at the centre is subtended by an arc of length l unit then θ =lr Given that r=75cm And here, l=10cm Hence substituting the values in the formula, θ =1075 radian =215radian

(ii) 15 cm

Ans: We know that, in a circle of radius r unit, if an angle θ radian at the centre is subtended by an arc of length l unit then θ =lr Given that r=75cm And here, l=15cm Hence substituting the values in the formula, θ =1575 radian =15radian

(iii) 21 cm

Ans: We know that, in a circle of radius r unit, if an angle θ radian at the centre is subtended by an arc of length l unit then θ =lr And here, l=21cm Hence substituting the values in the formula, θ =2175 radian =725radian

Exercise 3.2

1. Find the values of the other five trigonometric functions if cos x=-1/2 , x lies in the third quadrant.

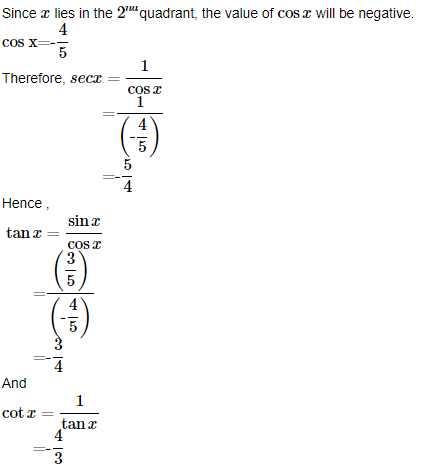
2. Find the values of other five trigonometric functions if sin x=3/5 , x lies in second quadrant.

3. Find the values of other five trigonometric functions if cot x=3/4 , x lies in third quadrant.

4. Find the values of other five trigonometric functions if sec x=13/5 , x lies in fourth quadrant.

5. Find the values of other five trigonometric functions if tan x=-512 , x lies in second quadrant.

6. Find the value of the trigonometric function sin765o

Ans: We know that the values of sinx repeat after an interval of 2π or 360∘ . Therefore we can write, sin765o=sin(2 × 360o+45o) =sin45o =1/√2–.

7. Find the value of the trigonometric function cosec(-1410o)

Ans: We know that the values of cosec x repeat after an interval of 2 π or 360∘ . Therefore we can write, cosec(-1410o)=cosec(-1410o+4 × 360o) =cosec(-1410o+1440o) =cosec30o =2

8. Find the value of the trigonometric function tan19π/3 .

Ans: We know that the values of tan x repeat after an interval of π or 180∘. Therefore we can write,

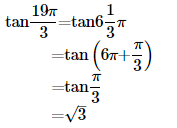
9. Find the value of the trigonometric function sin(-11π/3)

Ans: We know that the values of sin x repeat after an interval of 2 π or 360∘ . Therefore we can write,

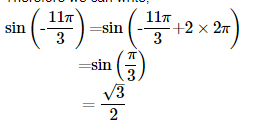
10. Find the value of the trigonometric function cot(-15π/4)

Ans: We know that the values of cot x repeat after an interval of π or 180∘. Therefore we can write,

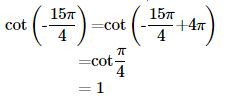
Exercise 3.3

5. Find the value of :

(i) sin75o

(ii) tan15o

22. Prove that cot x cot 2x-cot 2x cot 3x-cot 3x cot x=1

24. Prove that cos 4x=1-8sin2xcos2x

Ans: We know that, cos 2x=1-2sin2x And sin 2x=2sin x cos x L.H.S.=cos 4x =cos 2(2x) =1-2sin22x =1-2(2sin x cos x)2 Further computing we get, L.H.S=1-8sin2xcos2x =R.H.S. Hence proved.

25. Prove that cos 6x=32xcos6x-48cos4x+18cos2x-1

Ans: We know that, cos 3A=4cos3A-3cosA and cos 2x=1-2sin2x L.H.S.=cos 6x =cos 3(2x) =4cos32x-3cos 2x =4[(2cos2x-1)3-3(2cos2x-1)] Further computing, L.H.S=4[(2cos2x)3-(1)3-3(2cos2x)]-6cos2x+3 =4[(2cos2x)3-(1)3-3(2cos2x)2+3(2cos2x)]-6cos2x+3 =4[8cos6x-1-12cos4x+6cos2x]-6cos2x+3 =32cos6x-48cos4x+18cos2x-1 Therefore we have, L.H.S = R.H.S. Hence proved.

Exercise 3.4

1. Find the principal and general solutions of the tan x=3–√

2. Find the principal and general solutions of the equation secx=2

3. Find the principal and general solutions of the equation cot x=-3–√

Ans: Here it is given that, cot x=-3–√ Now we know that cot π/6=√3

4. Find the general solution of cosec x=-2

Ans: Here it is given that, cosec x=-2 Now we know that cosec π 6=2 and

5. Find the general solution of the equation cos 4x=cos 2x

6. Find the general solution of the equation cos 3x+cos x-cos 2x=0.

7. Find the general solution of the equation sin 2x+cos x=0.

Ans: Here it is given that, sin 2x cos x=0 Now we know that, sin 2x=2sin x cos x Therefore we have, 2sin x cos x+cos x=0 Which implies, cos x(2sin x+1)= 0 Therefore we have, Either cos x=0

8. Find the general solution of the equation sec22x=1-tan 2x

Last Updated on: Mar 28, 2024