Chapter 6 Work, Energy, and Power Questions and Answers: NCERT Solutions for Class 11th Physics (Partnership Physics )
Class 11 Physics (Partnership Physics ) Chapter 6: Work, Energy, and Power - Questions and Answers of NCERT Book Solutions.
1. The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative: work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
Ans: Positive.
Work done is the dot product of force and displacement. This means that the work will be positive if the projection of one of them on the other is in the same direction as the other. In other words, if the two vectors make an acute angle, then the work done is positive. Here, the bucket is being lifted upwards, which is in the same direction of the pull-force being applied. Hence the work done is positive.
b.work done by gravitational force in the above case,
Ans: Negative.
The gravitational force is acting downward, and the displacement is upwards, which means the angle these make ∼180∘
∼180∘
(obtuse). This means that the dot product of the two vectors would be negative.
c.work done by friction on a body sliding down an inclined plane,
Ans: Negative.
The direction of frictional force is opposite to the direction of motion; hence the work done by the frictional force is negative in this case.
d.work done by an applied force on a body moving on a rough horizontal plane with uniform velocity,
Ans: Positive.
The frictional force is acting in the direction opposite to the motion of the body. However, to maintain the constant velocity, extra force is applied in the direction of the motion. So this means that the work done by this extra force is positive.
e.work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Ans: Negative.
The resistive force always acts in the direction opposite to the motion of the body (pendulum). Thus the work done by this force is also negative.
2. A body of mass 2 kg
2 kg
initially at rest moves under the action of an applied horizontal force of 7N
7N
on a table with coefficient of kinetic friction =0.1
=0.1
. Compute the
a.work done by the applied force in 10s
Ans: Given the mass of the body, m=2kg
m=2kg
The force applied on the body, F=7N
F=7N
The given coefficient of kinetic friction, μ=0.1
μ=0.1
The initial velocity of the body, u=0
u=0
Time, t=10s
t=10s
The acceleration produced in the body by the applied force is given by Newton’s second law
of motion as:
a′=F/m=7/2=3.5 ms−2
a′=F/m=7/2=3.5 ms−2
And the frictional force is given as: f=μmg=0.1×2×9.8=1.96N
f=μmg=0.1×2×9.8=1.96N
The acceleration produced by the frictional force:
a′′=1.96/2=0.98 ms−2
a″=1.96/2=0.98 ms−2
Total acceleration of the body is the sum of the two accelerations: a′+a′′=3.5+0.98 ms−2
a′+a″=3.5+0.98 ms−2
Using the total acceleration, the distance traveled by the body is given by the equation of motion:
s=ut+1/2at2=0+1/2×2.52×102=126m
s=ut+1/2at2=0+1/2×2.52×102=126m
b.Work done by the applied force (F),
Wa=F.s=7×126=882J
Wa=F.s=7×126=882J
.
Hence the work done by the applied force is 882J.
work done by friction in 10s
10s
,
Ans: The work done by the frictional force (f),
Wf=f.s=−1.96×126=−247J
Wf=f.s=−1.96×126=−247J
.
c.work done by the net force on the body in 10s
10s
,
Ans: The net force acting on the body=7+(1.96)=5.04N
=7+(1.96)=5.04N
Hence the work done by the net force in the 10s, is equal to the product of the force and the distance travelled by the body, WNet=5.04×126=635J
WNet=5.04×126=635J
.
d.change in kinetic energy of the body in 10s
10s
, and interpret your results
Ans: Using the first equation of motion, final velocity can be calculated as:
v=u+at=0+2.52×10=25.2 m/s
v=u+at=0+2.52×10=25.2 m/s
The change in kinetic energy is
=1/2mv2−1/2mu2=1/2m(v2−u2)=635J
=1/2mv2−1/2mu2=1/2m(v2−u2)=635J
Hence the change in the kinetic energy is obtained as 635J.
3. Given in figure are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
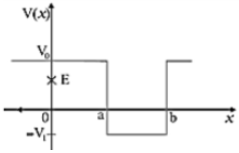
Ans.
The kinetic energy (T) of a body is given as the difference in the total energy of a system (E) and the potential energy (V):
T=E−V
T=E−V
Kinetic energy of a body is dependent on its mass and the square of its velocity. Neither of these quantities can be negative, hence Kinetic energy is also a positive quantity.
Therefore, the particle cannot exist in a region where T becomes negative or when V>E
V>E
.
For distance more than a, i.e., for x>a
x>a
, the Kinetic energy becomes negative, hence the case is not possible.
The minimum energy required is equal to the maximum potential energy shown i.e., E should be at least equal to V0
V0
All throughout, the total energy E is smaller than the potential energy V. Hence the kinetic energy is negative, which isn’t possible in a physical case. Hence a particle can’t be found for the given energy. The minimum energy required is equal to the maximum potential energy shown i.e., the E should be at least equal to V3
V3
For distance xb
x>b
, the kinetic energy becomes negative. Hence the scenario is not possible. However, for b>x>a
b>x>a
, the kinetic energy is either positive or zero. This is possible.
But for the particle to stay anywhere in the system, the minimum energy required is equal to the maximum potential energy is shown, i.e., E should be at least equal to V0
V0
.
For b/2
b/2
the potential energy of the particle becomes greater than the total energy. Hence the particle can’t stay here.
However, it can stay everywhere else. In case the particle is needed in this region, then the minimum total energy in this case would be V0
V0
.
However, it can stay everywhere else. In case the particle is needed in this region, then the minimum total energy in this case would be V0 V0 .
4. The potential energy function for a particle executing linear simple harmonic motion is given byV(x)=kx2/2
V(x)=kx2/2
, where k is the force constant of the oscillator. For k=0.5N/m
k=0.5N/m
, the graph of V(x)
V(x)
versus x is shown in the given Fig. Show that a particle of total energy 1J
1J
moving under this potential must ‘turn back’ when it reaches x=±2m
x=±2m
.
Ans: As given, the total energy of the particle, E= 1 J
E= 1 J
The potential energy of the particle V(x)=kx2/2
V(x)=kx2/2
The force constant of the oscillator is k=0.5Nm−1
k=0.5Nm−1
The total energy is: E=V+T
E=V+T
where T is the Kinetic energy of the particle. According to the conservation law, this energy does not change throughout the motion.
⇒1=1/2mv2+1/2kx2
⇒1=1/2mv2+1/2kx2
When the pendulum ‘turns back’, velocity (and hence T) becomes zero.
⇒1=1/2kx2
⇒1=1/2kx2
⇒x=±2
⇒x=±2
Hence, the particle turns back when it reaches x=±2
x=±2
5. Answer the following:
a.The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?
Ans: Rocket.
Total energy is given by the relation:
TE=PE+KE=12mv2+mghTE=PE+KE=12mv2+mgh
Now, when the casing of a rocket burns due to friction, the mass of the rocket gets reduced, which further causes the total energy to reduce. Clearly, it is at the cost of the rocket that the heat needed for burning is generated.
b.Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?
Ans: Gravitational force is a conserved force, which means that the work done by this force is independent of the path taken by the object. This means that if an object comes back to a place where it started from, i.e. when the total displacement is zero (i.e., a closed path), the work done is zero.
c.An artificial satellite orbiting the earth in a very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?
Ans: The atmospheric resistance costs the satellite its total energy. This means that the total energy keeps decreasing. So even when the kinetic energy increases due to the increase in the speed, the potential energy decreases much faster, leading to an overall drop in the energy.
So basically, the energy of the satellite is given as the sum of its kinetic energy, its potential energy, and the energy it loses to the atmospheric resistance.
d.In (i), the man walks 2m
2m
carrying a mass of 15kg
15kg,
on his hands. In (ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley and a mass of 15kg
15kg
hangs at its other end. In which case is the work done greater?
Ans: In the case where the person is carrying the weight horizontally, which means he has applied the force (F) in the vertically upward direction, but the displacement (s) is horizontal. The work done (W) is given by W=F.s=Fscosθ
W=F.s=Fscosθ
and the θ
θ
is the angle between the two vectors. Since θ=90∘
θ=90∘
the work becomes zero.
Similarly, in the second case, the person is pulling the rope horizontally and the motion of the weight is upwards, and hence the two vectors are perpendicular to each other. Hence the work is zero.
6. Underline the correct alternative:
a.When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.
Ans: decreases.
The body moves towards the lower potential hence decreasing the potential energy of the body.
b.Work done by a body against friction always results in a loss of its kinetic/potential energy.
Ans: Kinetic energy.
Friction usually reduces the velocity of the body and hence reduces the Kinetic energy as well.
c. The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system.
Ans: External force.
Internal forces cannot produce any change in the total momentum of a body. It’s a fact that the sum of all the internal forces is zero. Hence, the total momentum of a many- particle system is proportional to the external forces acting on the system.
d.In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies
Ans: Total linear momentum.
The momentum can neither be created nor destroyed. However the energies can change their forms.
7. State if each of the following statements is true or false. Give reasons for your answer. a. In an elastic collision of two bodies, the momentum and energy of each body is conserved.
Ans: False
Law of conservation of momentum states that the total momentum of the system is conserved when there is no net external force applied on the system. The momentum of one body can be transferred to other body in the system.
b.Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
Ans: False
Any external force on a body can change the total energy of the body.
c. Work done in the motion of a body over a closed loop is zero for every force in nature.
Ans: False
Total energy over a closed-loop motion is only zero if the force involved is conservative. Eg. The friction would do zero work in a closed-loop.
d.In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.
Ans: True
In inelastic collisions, the total energy is usually lost as sound or heat or vibrations which means that the initial kinetic energy is more than the final kinetic energy
8. Answer carefully, with reasons:
a. In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
Ans: No
At the point of contact, the moving billiard ball drops its velocity to zero and is still in the process of transferring its momentum and energy to the next ball. At this moment, the ball, which came to a sudden stop after hitting the next ball, has transferred its kinetic energy to the potential energy (of vibration), which is then transferred to the next ball as its kinetic energy.
b.Is the total linear momentum conserved during the short time of an elastic collision of two balls?
Ans: Yes
In an elastic collision, the total linear momentum is always conserved at every point in time.
c.What are the answers to (a) and (b) for an inelastic collision?
Ans: No, Yes.
There is a definite loss of kinetic energy in inelastic collisions, which happens during the collision. This is another reason why the total kinetic energy is not conserved.
The law of conservation of momentum is applicable to both elastic and inelastic collisions. Hence the total linear momentum is always conserved throughout the collision.
d.If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).
Ans: Elastic.
If the potential energy is only dependent on the separation distance, this means that the induced force is independent of the path that is taken by the balls. Hence the force is conservative. This means that the collisions here are also going to be elastic.
9. A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
Ans: It is given that the body is accelerated with a constant value-a
a
hence the corresponding force experienced is F=ma
F=ma
.
Let’s say that the initial velocity of the body is u
u
.
Thus, the velocity- v
v
of the body at any given point in time- t
t
can be written as v−u=at
v−u=at
And the power is
P=F.v=(ma)v
P=F.v=(ma)v
⇒P=ma(at+u)=ma2t+mau
⇒P=ma(at+u)=ma2t+mau
The mass, acceleration, and initial velocity are constant.
⇒P∝t
⇒P∝t
Hence it can be noted that power is linearly dependent on t.
10. A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to
(i)t1/2(ii)t(iii)t3/2(iv)t2
(i)t1/2(ii)t(iii)t3/2(iv)t2
Ans: In this case, the power is constant:
P=F.v=(ma)v
P=F.v=(ma)v
Since the mass of the body doesn’t change, the acceleration and the velocity are inversely proportional.
⇒a=Fmv
⇒a=Fmv
Also,
dvdt=a
dvdt=a
Equating the two accelerations
dvdt=a=Fmv
dvdt=a=Fmv
⇒mF∫vdv=∫dt
⇒mF∫vdv=∫dt
⇒mFv2=t+C
⇒mFv2=t+C
⇒v∝t1/2
⇒v∝t1/2
Hence the option (i) is valid.
11. A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by F=(−i^+2j^+3k^)N
F=(−i^+2j^+3k^)N
Where i, j, k are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis?
Ans: Force exerted on the body, F=(−i^+2j^+3k^)N
F=(−i^+2j^+3k^)N
.
Displacement, s=4k^m
s=4k^m
.
Hence the work done, W=F.s=(−i^+2j^+3k^).(4k^)=12J
W=F.s=(−i^+2j^+3k^).(4k^)=12J
.
Therefore it is concluded that the work done is 12J
12J
12. An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV
10 keV
, and the second with 100 keV
100 keV
.Which is faster, the electron or the proton? Obtain the ratio of their speeds. (electron mass me=9.11×10−31kg
me=9.11×10−31kg
, proton mass mp=1.67×10−27kg
mp=1.67×10−27kg
,eV= 1.60×10−19J
eV= 1.60×10−19J
) .
Ans: The given mass of the electron, me=9.11×10−31kg
me=9.11×10−31kg
and that of the proton is mp=1.67×10−27kg
mp=1.67×10−27kg
.
The given kinetic energy of the electron is Te=10keV=1.60×10−15J
Te=10keV=1.60×10−15J
, and the kinetic energy of the proton is Tp=100keV=1.60×10−14J
Tp=100keV=1.60×10−14J
.
The velocity of the electron is hence obtained as: ve=(2Teme)1/2=5.93×107m/s
ve=(2Teme)1/2=5.93×107m/s
Similarly, the velocity of the proton can be obtained as vp=(2Tpmp)1/2=4.38×106m/s
vp=(2Tpmp)1/2=4.38×106m/s
The ratio of their velocities is vevp=13.541
vevp=13.541
Hence the electron moves 13.54 times faster.
13. A rain drop of radius 2 mm
2 mm
falls from a height of 500 m
500 m
above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is 10m/s
10m/s
?
Ans: The given radius of the raindrop, r=2×10−3m
r=2×10−3m
The volume of the drop isV=(4/3)πr3
V=(4/3)πr3
And hence the mass is m=ρV=ρ(4/3)πr3
m=ρV=ρ(4/3)πr3
Therefore the gravitational force is F=mg=ρ(4/3)πr3g
F=mg=ρ(4/3)πr3g
Thus the work by gravitation in the first half of the journey of the drop: W1=F.s=0.082J
W1=F.s=0.082J
and here s=250m
s=250m
This is equal to the amount of work done in the second half of the journey, W2=0.082J
W2=0.082J
If there is no resistance force, then the total energy of the raindrop will remain the same. Hence the total energy on the top is: ET=mgh+0=0.164J
ET=mgh+0=0.164J
.
The resistive force makes the drop have a velocity of 10m/s
10m/s
. Hence the total energy at the ground:
EG=(1/2)mv2=1.675×10−3J
EG=(1/2)mv2=1.675×10−3J
Therefore the energy lost in the resistance is the difference between the energies: =ET−EG=−0.162J
=ET−EG=−0.162J
Hence the energy due to the resistive force is -0.162J.
14. A molecule in a gas container hits a horizontal wall with speed 200m/s
200m/s
and angle 30o
30o
with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?
Ans: The momentum of any system remains conserved as long as there aren’t any external forces acting on the system. Similarly, the momentum of the system in the gas container remains conserved irrespective of the collision being elastic or inelastic.
As the gas molecules strike the stationary wall of the container, they rebound at the same speed. Thus the velocity of the wall remains zero. This means that the collision is elastic. Hence, the total kinetic energy of the molecule remains conserved during the collision.
15. A pump on the ground floor of a building can pump up water to fill a tank of volume 30m3
30m3
in 15min
15min
. If the tank is 40m
40m
above the ground, and the efficiency of the pump is 30%
30%
, how much electric power is consumed by the pump?
Ans: Volume that can be filled in 15 minutes: V=30m3
V=30m3
And the time of operation, t=15min=900s
t=15min=900s
.
The tank is at h=40m
h=40m
height
And the given pump is of the efficiency η=30%=0.3
η=30%=0.3
.
The average power required for lifting the water to this height is:
P=Et=mght=13.067×103W
P=Et=mght=13.067×103W
This is the required power output, so we need a pump whose power output needs to be equal to this. In other words, the 30%
30%
of the pump's output should be equal to the required power.
P=30%Ppump
P=30%Ppump
⇒Ppump=100P30=43.6×103W=43.6kW
⇒Ppump=100P30=43.6×103W=43.6kW
Hence we need a pump that consumes 43.6kW
43.6kW
16. Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V . If the collision is elastic, which of the following figure is a possible result after collision?
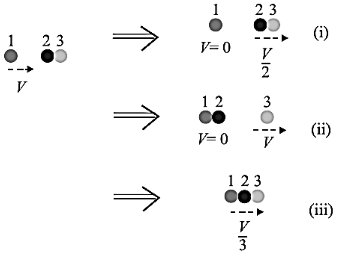
Ans: In all the cases of collisions where there is no external force, the linear momentum of the system is unchanged. In the case of elastic collision, the kinetic energy is also conserved.
Let’s say that all the ball bearings have mass- m
, so the total kinetic energy before collision:
Ti=12mV2+12m02+12m02=12mV2
Ti=12mV2+12m02+12m02=12mV2
Now, one needs to check that the final kinetic energy is equal to the initial one.
Case i)
The final kinetic energy Tf=12m02+12m(V2)2+12m(V2)2=14mV2
Tf=12m02+12m(V2)2+12m(V2)2=14mV2
.
Case ii)
The final kinetic energy isTf=12m02+12m02+12mV2=12mV2
Tf=12m02+12m02+12mV2=12mV2
.
Case iii)
The final kinetic energy is Tf=12m(V3)2+12m(V3)2+12m(V3)2=16mV2
Tf=12m(V3)2+12m(V3)2+12m(V3)2=16mV2
Hence it is clearly seen that the kinetic energy is conserved only in case (ii).
17. The bob A of a pendulum released from30o
30o
to the vertical hits another bob B of the same mass at rest on a table as shown in figure. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.
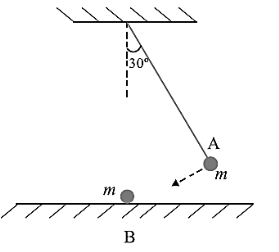
Ans: It is given that,
Mass of each ball=0.05kg=0.05kg
Initial velocity of each ball=6m/s=6m/s
Magnitude of the initial momentum of each ball, pi=0.3kgms−1pi=0.3kgms−1
After collision, the balls change their directions of motion without changing the
magnitudes of their velocity.
Final momentum of each ball, pf=−0.3kgms−1pf=−0.3kgms−1
Impulse imparted to each ball== Change in the momentum of the system
⇒Impulse=pf−pi⇒Impulse=pf−pi
⇒Impulse=−0.3−0.3=−0.6kgms−1⇒Impulse=−0.3−0.3=−0.6kgms−1
The negative sign indicates that the impulses imparted to the balls are opposite in direction.
18. The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?
Ans: As provided, the length of the pendulum, l=1.5m
l=1.5m
The mass of the bob =m
=m
Energy dissipated = 5
= 5
The law of conservation of momentum states the linear momentum of a system is unchanged in the absence of external force.
In the horizontal position
The PE of the bob is EP=mgl
EP=mgl
, while the KE is EK=0
EK=0
and hence the total energy is E=mgl
E=mgl
While at the lowermost point or the mean position, the potential energy is EP=0
EP=0
, the KE is EK=12mv2
EK=12mv2
, and the total energy is E=12mv2
E=12mv2
.
But the bob loses 5% of its energy.
Hence the total energy at the lowermost point is 95% of the total energy at the higher/horizontal position
⇒12mv2=95100mgl
⇒12mv2=95100mgl
⇒v=5.28m/s
⇒v=5.28m/s
.
Hence the bob arrives with 5.28m/s at the lowest point.
19. A trolley of mass 300kg
300kg
carrying a sandbag of 25kg
25kg
is moving uniformly with a speed of 27km/h
27km/h
on a frictionless track. After a while, sand starts leaking out of a hole on the floor of the trolley at the rate of. 0.05 kg/s
0.05 kg/s
. What is the speed of the trolley after the entire sand bag is empty?
Ans: As the trolley carrying the sand bag is moving without friction, which means, there is no friction which can act as an external force on the system. Hence the law of conservation of momentum is applicable.
The given initial mass of the bag ms(t=0)=25kg
ms(t=0)=25kg
and of the trolley ismTr=300kg
mTr=300kg
, hence the total initial mass is MTot(t=0)=325kg
MTot(t=0)=325kg
. And the mass drop rate is dMdt=0.05kg/s
dMdt=0.05kg/s
.
The initial velocity of the trolley is v(t=0)=27km/h=7.5m/s
v(t=0)=27km/h=7.5m/s
The momentum at any given time t
t
is p=(325−0.05t)v(t)
p=(325−0.05t)v(t)
and at t=0
t=0
, the momentum p(t=0)=325v(t=0)=325×27=8775kgm/s
p(t=0)=325v(t=0)=325×27=8775kgm/s
The time at which the sandbag empties, tfinal=250.05=500s
tfinal=250.05=500s
Thus the momentum at tfinal
tfinal
can be written as
8775=(325−0.05×500).v(tfinal=500)
8775=(325−0.05×500).v(tfinal=500)
⇒8775=300.v(tfinal)
⇒8775=300.v(tfinal)
⇒v(tfinal)=29.25m/s
⇒v(tfinal)=29.25m/s
Hence the final velocity when the bag is emptied is 29.25m/s
29.25m/s
.
20. A body of mass m=0.5kg
m=0.5kg
travels in a straight line with velocity v=ax3/2
v=ax3/2
where a=5m1/2s−1
a=5m1/2s−1
. What is the work done by the net force during its displacement from x=0
x=0
to x=2
x=2
?
Ans: The given mass of the body is m=0.5kg
m=0.5kg
and is moving with velocityv=ax3/2
v=ax3/2
where a=5m1/2s−1
a=5m1/2s−1
.
The kinetic energy at x=0
x=0
is EK(x=0)=120.5×0
EK(x=0)=120.5×0
and at x=2
x=2
is EK(x=2)=120.5×(5×23/2)2=50J
EK(x=2)=120.5×(5×23/2)2=50J
.
The difference in these two values is equal to the work done.
W=EK(x=2)−EK(x=0)=50J
W=EK(x=2)−EK(x=0)=50J
Hence the work done is 50J
50J
.
.
21. The blades of a windmill sweep out a circle of area =A
a.If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t?
Ans: As provided, the circular area swept by the windmill =A
And the velocity of the wind is =v
=v
And the density of the air is =ρ
=ρ
The volume flow rate of wind through the windmill is=Av
=Av
And hence the mass flow rate is m/t=ρAv
m/t=ρAv
Hence the mass flowing in time t is m=ρAvt
m=ρAvt
.
What is the kinetic energy of the air?
Ans: Using this mass the kinetic energy is obtained as
=12mv2=12ρAv2t=Ewind
=12mv2=12ρAv2t=Ewind
This is also equal to the energy that the wind carries with itself.
Assume that the windmill converts 25
25
of the wind’s energy into electrical energy, and that A=30m2
A=30m2
, v=36km/h
v=36km/h
and the density of air is ρ=1.2kg/m3
ρ=1.2kg/m3
. What is the electrical power produced?
Ans: The area of the circle swept is A=30m2
A=30m2
And the given velocity is v=36km/h=10m/s
v=36km/h=10m/s
The density is ρ=1.2kg/m3
ρ=1.2kg/m3
Since the windmill converts only 25% of wind energy to electricity.
Eelectric=25
Eelectric=25
Hence the electric power is obtained as Pelectric=Eelectric/t=4.5kW
Pelectric=Eelectric/t=4.5kW
.
The electric power output from the windmill is 4.5kW.
22. A person trying to lose weight (dieter) lifts a 10kg
10kg
mass, one thousand times, to a height of 0.5m
0.5m
each time. Assume that the potential energy lost each time she lowers the mass is dissipated.
How much work does she do against the gravitational force?
Ans: Mass of the dumbbell m=10kg
m=10kg
The height up to which it is lifted h=0.5m
h=0.5m
Hence the work done with every lift ismgh
mgh
Number of times the dumbbell is liftedn=1000
n=1000
Hence the total work done against gravity is =nmgh=49kJ
=nmgh=49kJ
.
Fat supplies 3.8×107J
3.8×107J
of energy per kilogram which is converted to mechanical energy with a 20
20
efficiency rate. How much fat will the dieter use up?
Ans: Energy supplied with every kilogram of fat is3.8×107J
3.8×107J
The efficiency is20
20
Hence the mechanical energy supplied by the body
=201003.8×107J=7.6×106J
=201003.8×107J=7.6×106J
And the equivalent fat loss is 6.45×10−3kg
6.45×10−3kg
Hence the body loses 6.45×10−3kg
6.45×10−3kg
of fat.
23. A family uses 8kW
8kW
of power.
Direct solar energy is incident on the horizontal surface at an average rate of 200W
200W
per square meter. If 20
20
of this energy can be converted to useful electrical energy, how large an area is needed to supply 8kW
8kW
?
Ans: The given power requirement of a family isP=8kW=8×103W
P=8kW=8×103W
The solar energy per sq mts Psolar/A=200W
Psolar/A=200W
Efficiency in converting solar to electrical energy η=20
η=20
Let the area needed to generate the required electricity be A
A
Total solar power is Psolar=(Psolar/A).A
Psolar=(Psolar/A).A
And the expected electrical power output can be written asP=20
P=20
⇒A=200m2
⇒A=200m2
Hence the area required is A=200m2
A=200m2
.
Compare this area to that of the roof of a typical house.
Ans: A typical house can have a roof of the dimensions 15×15m2
15×15m2
, hence the area is ≥200m2
≥200m2
. And this is more than the required area.
24. A bullet of mass 0.012kg
0.012kg
and horizontal speed 70m/s
70m/s
strikes a block of wood of mass 0.4kg
0.4kg
and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
Ans: As provided, the mass of the bullet ism=0.012kg
m=0.012kg
And the initial speed of the bullet before hitting the block , ub=70m/s
ub=70m/s
Mass of the wooden block, M=0.4kg
M=0.4kg
The initial speed of the stationary wooden block, uB=0
uB=0
Let the final speed of the system of the bullet and the block be vb+B
vb+B
According to the law of conservation of momentum:
mub+MuB=(m+M)vb+B
mub+MuB=(m+M)vb+B
⇒vb+B=(0.012×70+0.4×0)0.012+0.4=2.04m/s
⇒vb+B=(0.012×70+0.4×0)0.012+0.4=2.04m/s
For the system of the bullet and the wooden block when they are stuck together:
The total mass of the system, Mb+B=0.412kg
Mb+B=0.412kg
And the resultant velocity of the system vb+B=2.04m/s
vb+B=2.04m/s
Height up to which the system rise=h
=h
Applying the law of conservation of energy to this system:
The potential energy at the highest point is equal to the Kinetic energy at the lowest point
Mb+Bgh=(1/2)Mb+Bvb+B2
Mb+Bgh=(1/2)Mb+Bvb+B2
⇒h=vb+B22g=0.2123m>
⇒h=vb+B22g=0.2123m
Hence the wooden block rises up to the height of 0.2123m
0.2123m
The energy lost in the form of heat is the drop in the energy of the bullet.
=12mub2−12Mb+Bvb+B2=29.4−0.857=28.54J
=12mub2−12Mb+Bvb+B2=29.4−0.857=28.54J
Hence the heat produced is 28.54J
28.54J
25. Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track (figure). Will the stones reach the bottom at the same time? Will they reach there with the same speed? Explain.
Given θ1=30o
θ1=30o
, θ2=60o
θ2=60o
and h=10m
h=10m
, what are the speeds and times taken by the two stones?
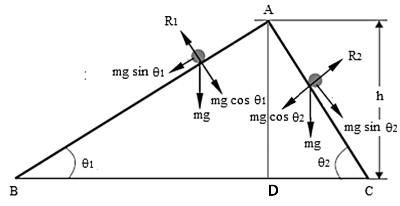
Ans: AB and AC are both smooth planes.
Intuitively it can be said that, as height of both the planes is the same, therefore, north the stones will reach the bottom with same speed. But since the side AB is longer, the stone will take more time to reach down.
The mathematics for the same is as follows
The potential energy at A is supposed to be equal to the kinetic energies of the stones when they reach B and C
mgh=12mv12=12mv22
mgh=12mv12=12mv22
⇒v1=v2
⇒v1=v2
The accelerations along the sides are given as
a1=gsinθ1
a1=gsinθ1
a2=gsinθ2
a2=gsinθ2
As θ2>θ1
θ2>θ1
, ⇒a2>a1
⇒a2>a1
Now since v=u+at=0+at
v=u+at=0+at
⇒t2t1
⇒t2t1
Hence the second stone will reach sooner than the first stone, which attains the same speed while reaching down but will take less time.
26. A 1 kg
1 kg
block situated on a rough incline is connected to a spring of spring constant 100N/m
100N/m
as shown in figure. The block is released from rest with the spring in the upstretched position. The block moves 10 cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.
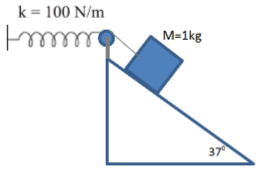
Ans: AS provided in the question, the mass of the block, M= 1 kg
M= 1 kg
Spring constant, k=100N/m
k=100N/m
Displacement in the block along the plane, x=0.1m
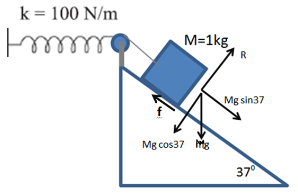
At equilibrium, the normal reaction is R=Mgcos37o
R=Mgcos37o
The friction force acting opposite to Mgsin37o
Mgsin37o
is f=μR=μMgcos37o
f=μR=μMgcos37o
Here the coefficient of friction is μ
μ
The net force acting on the block is 0, and its expression in terms of its components is: Mgsin37o−f=Mg(sin37o−μcos37o)
Mgsin37o−f=Mg(sin37o−μcos37o)
Also, the work done is equal to the potential energy of the spring
Mg(sin37o−μcos37o)x=(1/2)kx2
Mg(sin37o−μcos37o)x=(1/2)kx2
Hence the required coefficient of friction is
⇒μ=(sin37o−(1/2)kxMg)cos37o=0.115
⇒μ=(sin37o−(1/2)kxMg)cos37o=0.115
Therefore the coefficient of friction is 0.115
0.115
27. A bolt of mass 0.3kg
0.3kg
falls from the ceiling of an elevator moving down with an uniform speed of 7m/s
7m/s
. It hits the floor of the elevator (length of the elevator = 3m
3m
) and does not rebound. What is the heat produced by the impact? Would your answer be different if the elevator were stationary?
Ans: The given bolt has a mass of m=0.3kg
m=0.3kg
The elevator moves with speed v=7m/s
v=7m/s
And the height of the elevator is h=3m
h=3m
The relative velocity of the bolt wrt lift is zero; hence at the time of impact, the change in potential energy is converted to heat.
ΔPE=mgh=0.3×9.8×3=8.82J
ΔPE=mgh=0.3×9.8×3=8.82J
The heat produced is dependent on the relative velocity of the bolt wrt the elevator, and not on anything else. Hence the heat generated remains the same even if the elevator is moving.
28. A trolley of mass 200kg
200kg
moves with a uniform speed of v=36km
v=36km
on a frictionless track. A child of mass 20kg
20kg
runs on the trolley from one end to the other (10 m away) with a speed of 4m/s
4m/s
relative to the trolley in a direction opposite to the its motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
Ans: As provided, the trolley weighs M=200kg
M=200kg
and is l=10m
l=10m
long
It moves with a velocity of v=36km/h=10m/s
v=36km/h=10m/s
And the mass of the boy is m=20kg
m=20kg
The initial momentum of trolley+boy is (M+m)v=2200kgm/s
(M+m)v=2200kgm/s
Now let the final velocity be v′
v′
And the boy’s final velocity wrt ground isv′−4
v′−4
Hence the final momentum is
Mv′+m(v′−4)=220v′−80
Mv′+m(v′−4)=220v′−80
Since there is no external force, the final momentum is equal to the initial momentum
2200=220v′−80
2200=220v′−80
⇒v′=10.36m/s
⇒v′=10.36m/s
The boy’s speed is v′′=4m/s
v″=4m/s
The time taken to run across the trolley t=10/4=2.5s
t=10/4=2.5s
Hence the distance moved by the trolley isv′′t=25.9m
v″t=25.9m
29. Which of the following potential energy curves in figure cannot possibly describe the elastic collision of two billiard balls? Here r is the distance between centres of the balls.
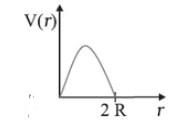
Ans: The gravitational potential energy of a system of two masses is inversely related to the separation between the two of them.
However, In the given case, the potential energy of the system of the two balls will decrease as they come closer to each other. It will become zero when the two balls touch each other, i.e., when the distance between the two is 2R.
The potential energy curves given in figures (i), (ii), (iii), (iv), and (vi) do not satisfy these two conditions, and hence they can’t describe the elastic collisions.
30. Consider the decay of a free neutron at rest:n→p++e−
n→p++e−
Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in decay the of a neutron or a nucleus (figure).
Ans: The given neutron decay at rest can be written as
n→p++e−
n→p++e−
According to Einstein's mass-energy relation, the mass lost (Δm
Δm
) will be taken by the ejected electron as energyΔmc2
Δmc2
. The mass defect (Δm
Δm
) is the difference in the mass of the neutron and the sum of the proton masses and electron.
Δm=mneutron−(mp++me−)
Δm=mneutron−(mp++me−)
The speed of light is denoted by c
c
Hence the equation misses showing the change in the mass or the energy and where it went. Adding an energetic neutrino ν
ν
on the RHS would solve the issue.
Last Updated on: Mar 28, 2024
