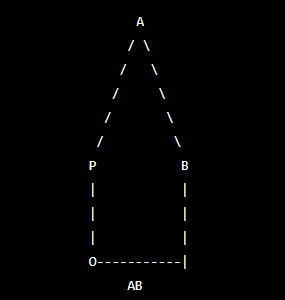
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ZAPB = 2 ZOAB.

Question :PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ZAPB = 2 ZOAB.

The correct answer :As per the problem, we have the following figure:

We need to prove that ZAPB = 2 ZOAB.

Let us consider triangle OAB.

In this triangle, we have OA = OB (radii of the same circle), and AB is a common side.

Therefore, by the side-side-side (SSS) congruence criterion, we can say that triangle OAB is an isosceles triangle.

Therefore, ZOAB = ZOBA.

Let ZAPB = x (as given in the problem).

Then, ZOAP = ZOAB – ZPAB = ZOAB – x (since PA is tangent to the circle, ZOAP = ZPAB).

Similarly, ZPBO = ZOBA – ZPAB = ZOAB – x.

Now, ZAOP + ZPOB + ZOAB = 180° (sum of angles of triangle AOB).

Substituting the values we have obtained above, we get:

(ZOAB – x) + (ZOAB – x) + ZOAB = 180°

Simplifying the above equation, we get:

3ZOAB – 2x = 180°

or 2x = 3ZOAB – 180°

or x = (3/2)ZOAB – 90°

Therefore, ZAPB = (3/2)ZOAB – 90°.

Now, substituting the value of ZOAB in terms of ZAPB in the above equation, we get:

ZAPB = (3/2)(ZAPB + 2ZOAB) – 90°

Simplifying the above equation, we get:

ZAPB = 2ZOAB

Hence, proved.